Notes On MIT18.875
参考了包括但不限于ProofWiki
Lec 1&2
注意到特征
- 在试图证1.5的时候我发现
等等,再考虑到仿照 的想法得到如下证明:由 ,有 同理 ,若 则可知 。 - 注意到有将
映到 的 嵌入。
如果
即 ,则欲证 只需证 ,即 。现在只需证 推出 ,而假若不然 时, ,但因为 左边是右边的高阶无穷大,矛盾。 假设
是一个 上的绝对值。首先证明存在 使得 ,则 非阿:取 ,把 关于 进制展开 因为 所以 以 代 则是 ,其中 ,使 得到 ,明所欲证。现在假设 阿基米德,任意 均满足 ,取 ,如上以 进制展开 ,令 ,则 ,从而 以 代 得到 ,使 得到 。由于 可以任取,令 ,则 ,而且因为阿基米德所以 ,进而给出 和 的等价。而如果 非阿,考虑赋值环 ,对应有极大理想 ,特别的, , 是 中素理想,从而为某个 。由此知,对一切与 相异的素数 , ,而 ,从而 。 考虑到
对
- 显然。
- 首先
- 显然。
- 先假设
- 只需注意到
- 和
- 和
- 考虑
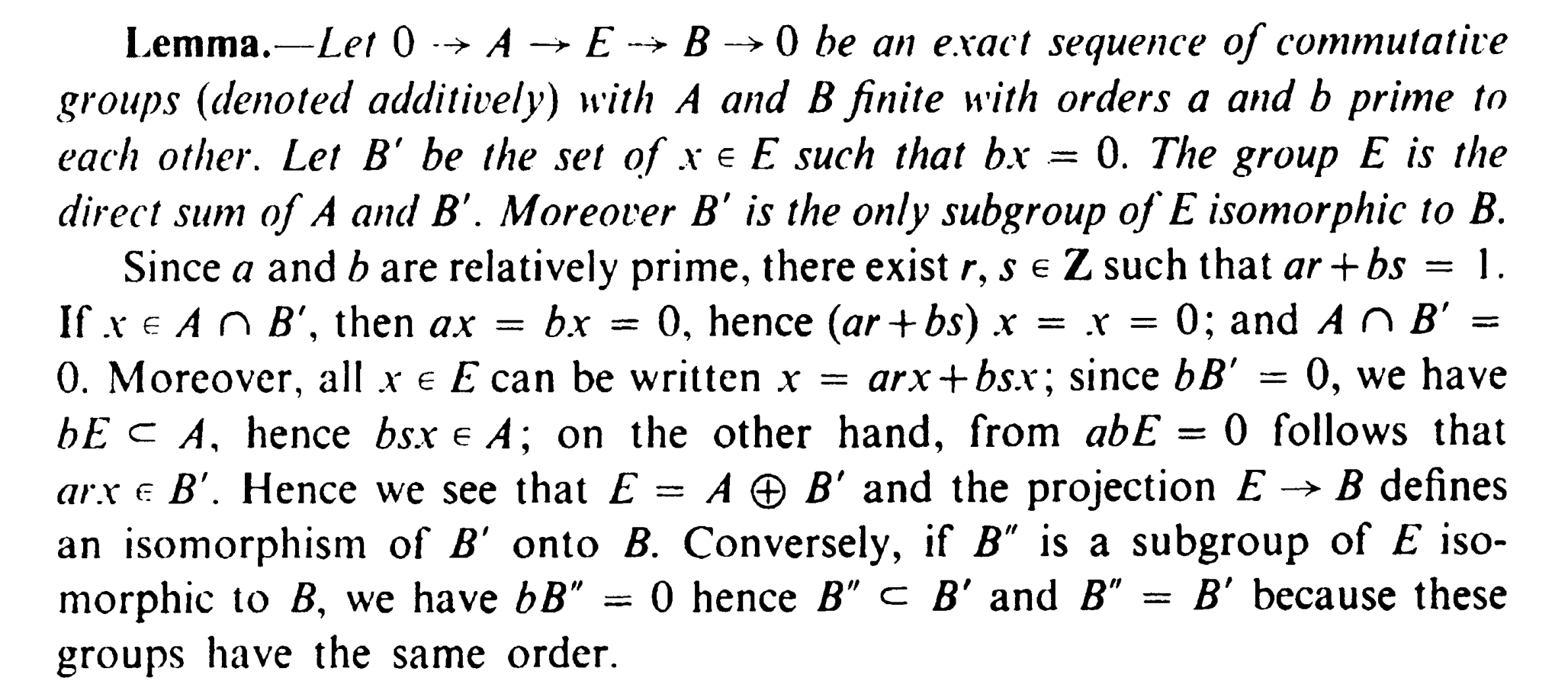 有
有 Missing superscript or subscript argument (A/b)^