基本性质
直观上来讲,双线性和对应着“乘法”,例如
如果模
L M £ N L 0 ' B B 0
模
和
的张量积则是“最基本的”乘法。
张量积 是
对任意模
唯一性由始对象的特质给出,也就是假设有两个张量积
存在性考虑
注:上面证明存在性处的具体构造除证明张量积存在以外毫无用处。
对一般非交换环情形,比如说对右
(交换约束)
映射
只需验证
同样的道理,注意到
对域
考虑
注:
由于
而反过来,乘法给出双线性映射
更一般的,用同样的手段我们可以证明
考虑乘法定义的映射
注:这个命题也可依靠张量积的右正合性证明,具体来说考虑
对
考虑双线性映射
(结合约束)
取某个
Reading: Section 2.2
张量积与正合列
如果
与tensor上
对反过来的
比如说对
同样对
注:事实上 Atiyah
Prop. 2.9 。
从正合列
注:上面证明中的自然同构告诉我们
这种右正合性可以用于计算张量积,具体来说比如说对于
张量积和余极限
与之类似的有用性质是张量积保持direct limit
N M j M i M k
两个锥
间的同态是使两个锥的图表带上这个映射之后的大图表交换的线性映射,容易验证这样我们定义了一个范畴。它的direct
limit
就是其上锥的始对象,具体泛性质如以下交换图
lim ¡ ! M i N M j M i M k 9 !
它可以被构造为诸
的直和商去关系
,这里
是
到
的映射,这些验证可以参见
Atiyah第二章习题14-19 。direct
limit就是模范畴上的余极限。
而关于张量积,
Reading: Section 2.2n ) where f is an irreducible polynomial.
平坦模
平坦模的概念由Serre在20世纪50年代引入,此后被Grothendieck证明在代数几何中具有极其基本的地位。直观来讲,
平坦模 如果
用构造局部化环完全相同的手段,我们可以定义局部化模
模的局部化保持正合(
考虑正合列
我们把
我们可以定义映射
对一些比较好的情况我们可以探测到一些平坦模的结构。例如
对
因为局部化正合,所以只需证明
想说明
注:如果把
Reading: Section 2.2
平坦扩张
环同态
不过如果
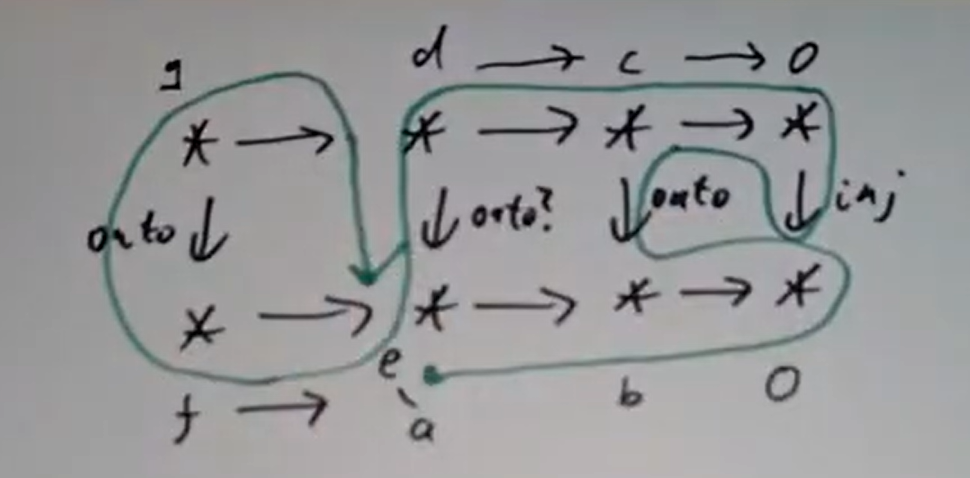
(5引理)对交换图
M 0 M 1 M 2 M 3 M 4 N 0 N 1 N 2 N 3 N 4
其中横行皆正合,有
考虑以如下路线追图
的追图则更简单。假设
假设
记
Reading: Section 2.2
 取
取