局部化的定义
直观上,
局部化 为满足如下泛性质的环
R A R [ S ¡ 1 ] ' ' [ S ¡ 1 ]
这种形式上取逆的做法事实上比较非构造性,让我们对
的大小失去了控制,比如我们难以直接知道哪些
中元素会在自然映射
下变成
。如果对
,存在
使
,那么
会被打到
,事实上自然映射
的核由被某个
作用得
的
组成。
直接考虑将 全商环(total quotient
ring) ,它是
更进一步的,对于
于是
Reading: Section 2.1
局部化的
如果
注意到若
如果
某种意义上可以将
首先
如果
一般来说
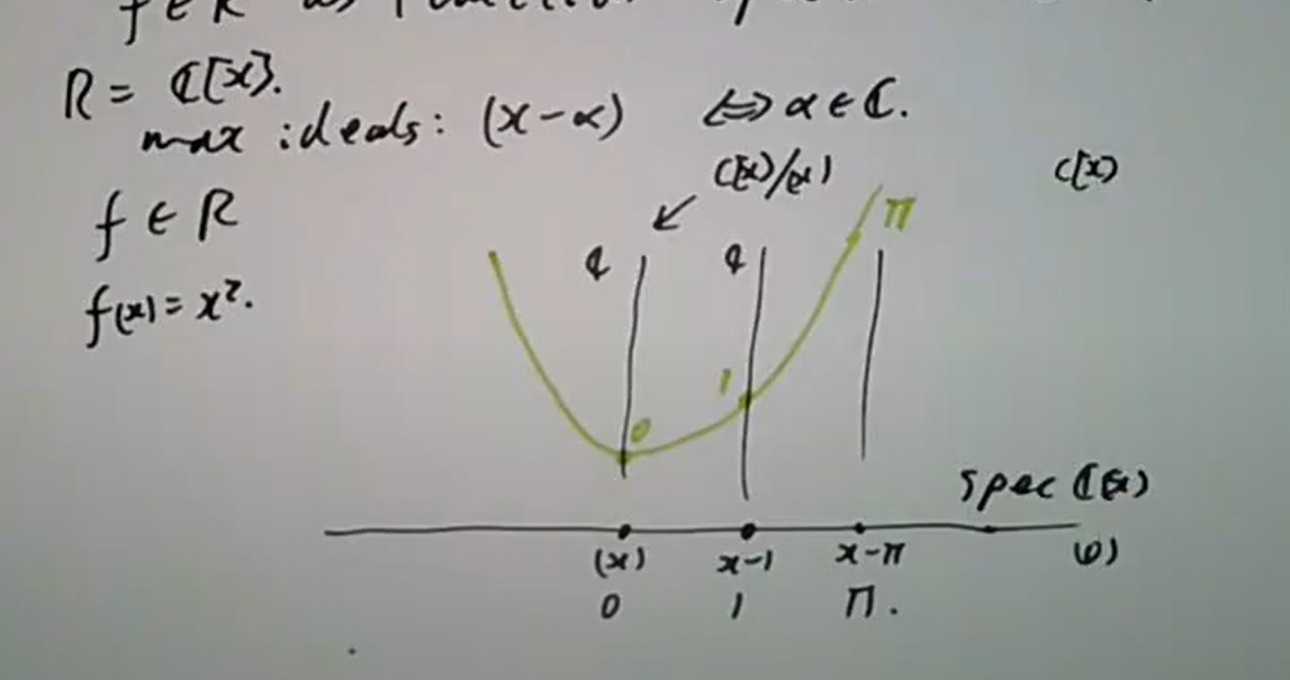
上一章3.10 已经有过可视化。关于
一般来讲,
Reading: Section 2.1
对紧Hausdorff空间
但这种函数化会出现一个问题,就是
事实上我们有更好的方法来表示出这样的函数,具体来说是使
我们希望对任意的环
直观上来说,
Exercise: 2.6
仿射概形
某种意义上仿射概形的观点在于将
具体来说 (1) 对含入映射(对应函数的限制)
假设
这里只考虑
仿射概形 。这种几何语言和交换环本身的代数语言之间具有一些对偶关系,具体来说
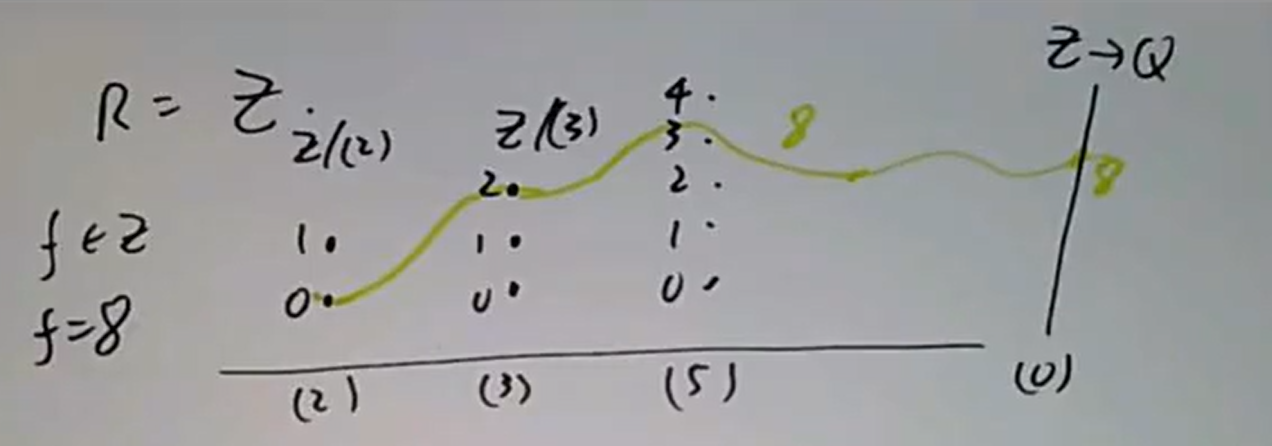
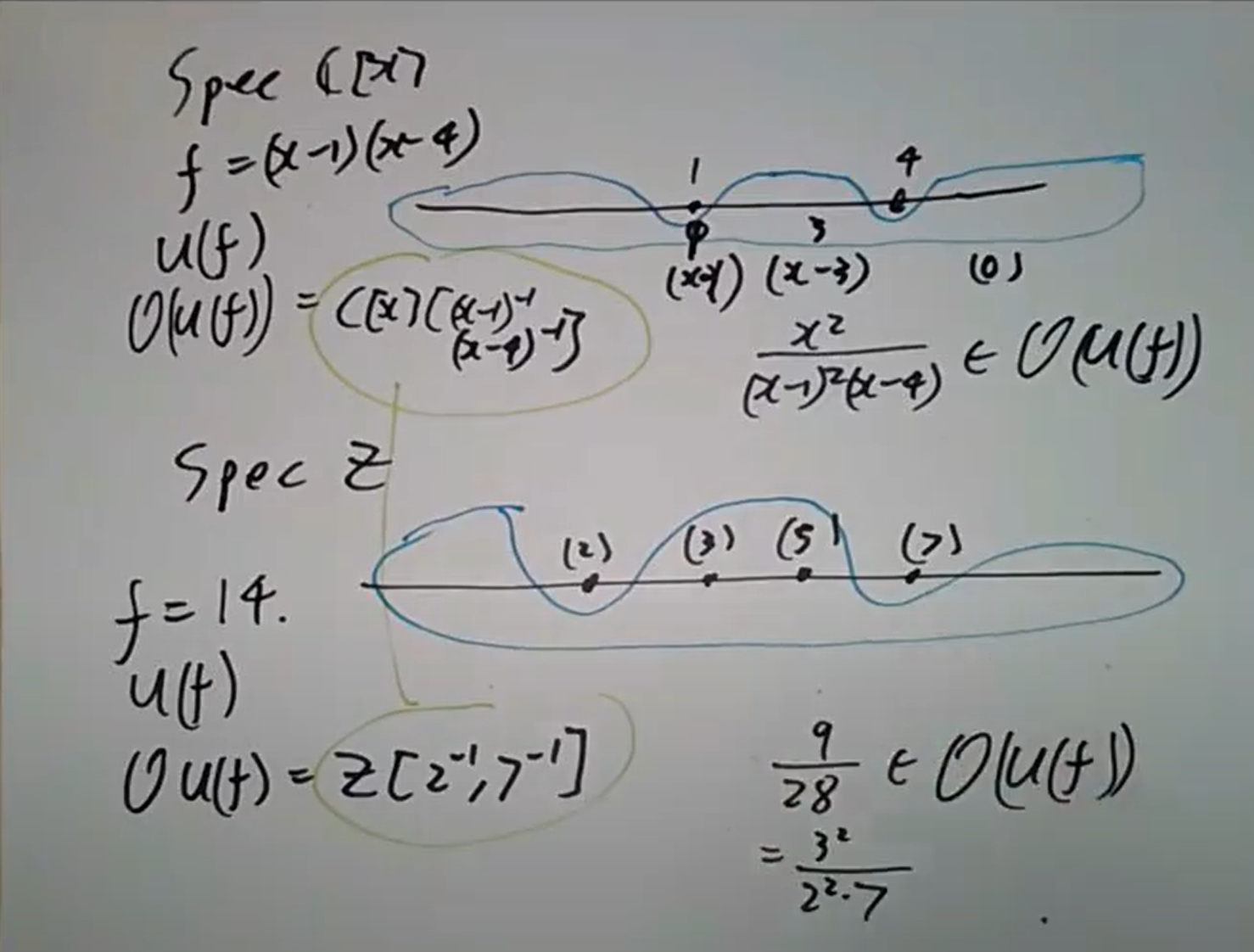
下面是一些基本例子
Exercise: 2.19, 2.26
 事实上
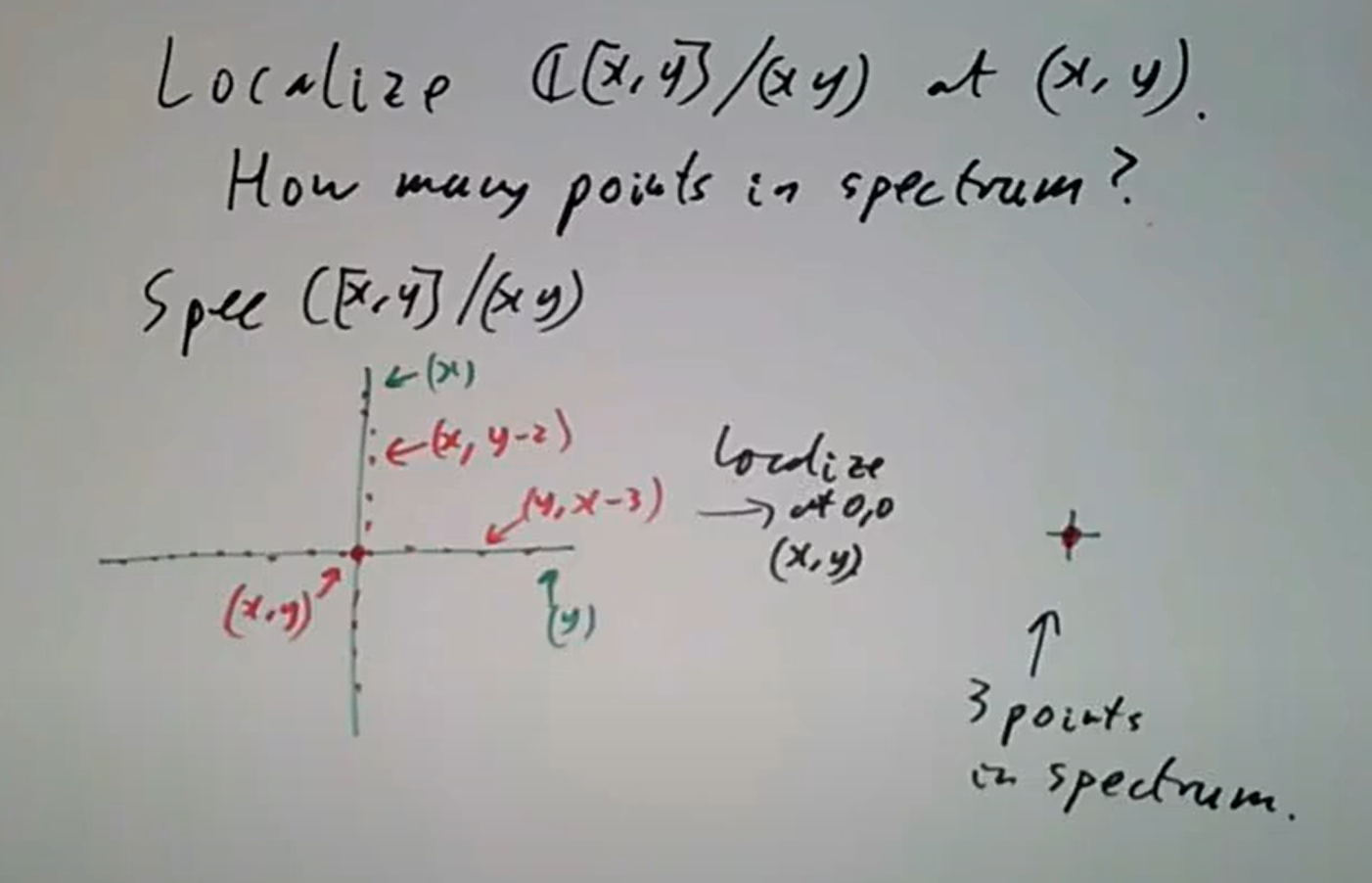
事实上 注意素理想局部化的素谱和商环的素谱大相径庭,譬如说
注意素理想局部化的素谱和商环的素谱大相径庭,譬如说