关于环的可视化,大体有三种比较直接的方法:画出环中每个元素、画出环的一组基和画出环的素理想。
环元素作为点的可视化
这种可视化适用于加群可嵌入线性空间的环,所以它对代数数域的代数整数环,从而对代数数论很有用。这种可视化最简单的例子如下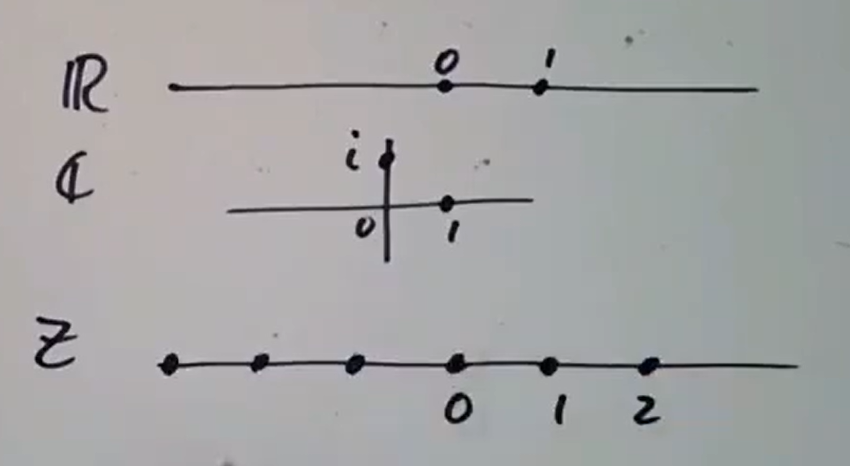 此外有高斯整数 的可视化
此外有高斯整数 的可视化 这种可视化手段的一个直接应用是:
这种可视化手段的一个直接应用是:
是欧几里得整环,从而是UFD
取
上继承的复数绝对值,我们将证明它给出一个符合ED公理的尺度函数(这里ED定义我们要求尺度函数是
到某个良序集的映射)。也就是说,对 且
,我们想证明存在 满足也即而我们只需考虑到如图所示,以某个
中元素为圆心,半径为1的开圆盘覆盖了复平面 则立即可知上述
的存在性。
则立即可知上述
的存在性。
类似的方法可以毫无阻碍地推广到
是欧几里得整环,从而是UFD
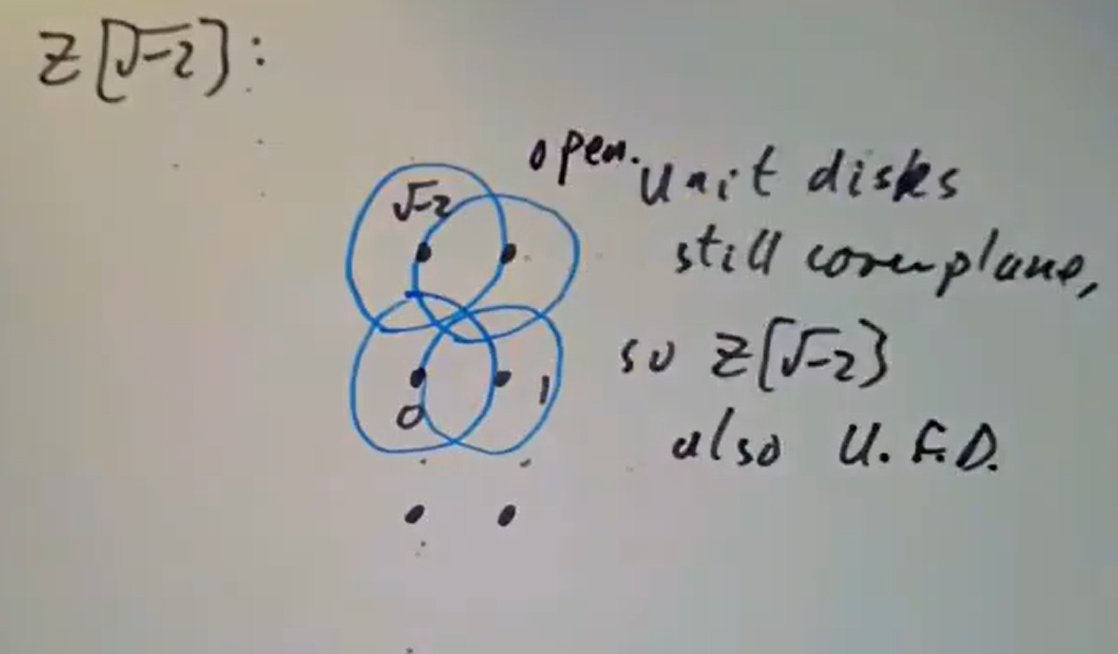 画图立即可知。
画图立即可知。
不过绝对值并非总是尺度函数,例如对 , 距 中整点距离至少是
。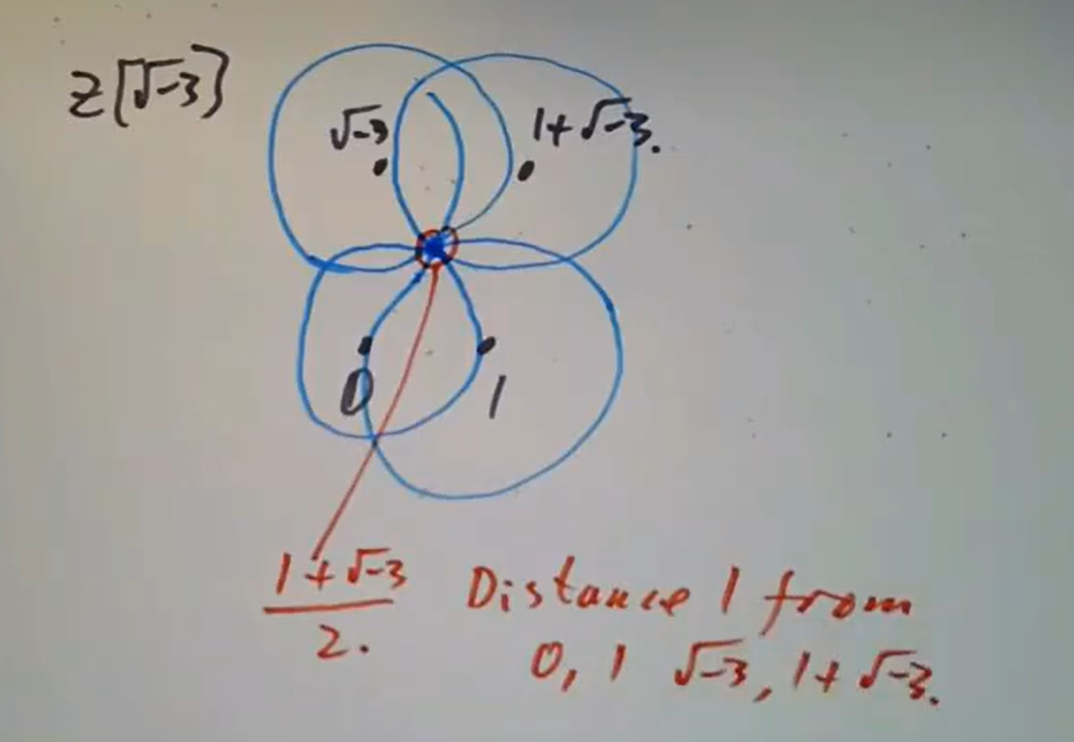 非但如此, 还可以证明一定不可能是ED,甚至不是UFD(只需注意到
给出不唯一的素因子分解)。也因此它有非主理想,事实上
就是一个例子,这一点的证明依然可以画图
非但如此, 还可以证明一定不可能是ED,甚至不是UFD(只需注意到
给出不唯一的素因子分解)。也因此它有非主理想,事实上
就是一个例子,这一点的证明依然可以画图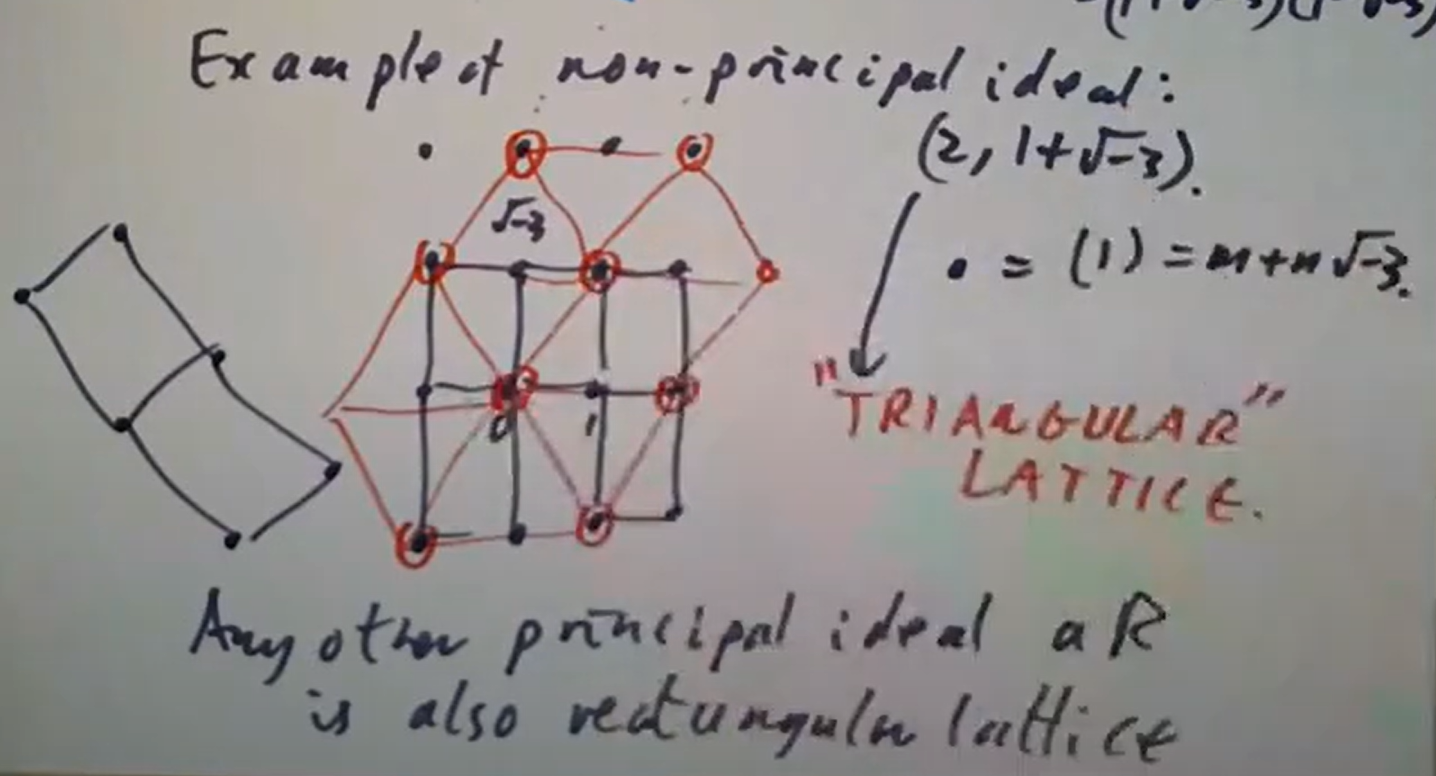 这里
是全部黑色格点(从而主理想都是这个矩阵格点旋转伸缩,所以也是矩阵形状的格点),而
是红色三角形格,并非矩形格点,因此不可能是主理想。
这里
是全部黑色格点(从而主理想都是这个矩阵格点旋转伸缩,所以也是矩阵形状的格点),而
是红色三角形格,并非矩形格点,因此不可能是主理想。
不过这个问题可以一定程度上“修复”。例如考虑 。如图所示,这显然是ED
某种意义上ED是稀有的,即使在UFD中也是如此。例如考虑 是UFD,则 也是UFD,但并不一定是PID(例如
,从而未必ED)。而实践中的PID大多是ED,例如 、 、 离散赋值环、 等,不过也有反例。
是PID,但不是ED,这点可以作如下考虑:假若它是ED,那么取某个尺度函数最小的不可逆元
,则 中元素都可以选取一个可逆或者是
的代表元,但 中可逆元只有 ,所以 至多只能有三个元素,但可以验证
对任意 都至少有四个元素。
环一组基作为点的可视化
Exercises: 1.18, 1.19
如果我们的环像 一样,是域
上线性空间,那么就可以通过它的一组基来可视化这个环,例如: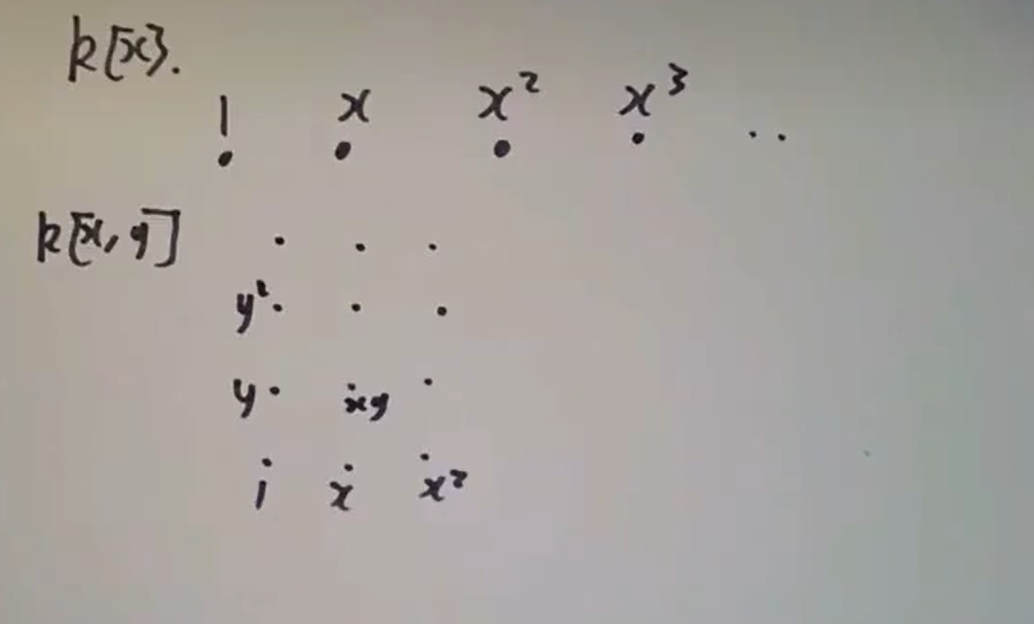
考虑
,我们只需要考虑把商掉的理想画出来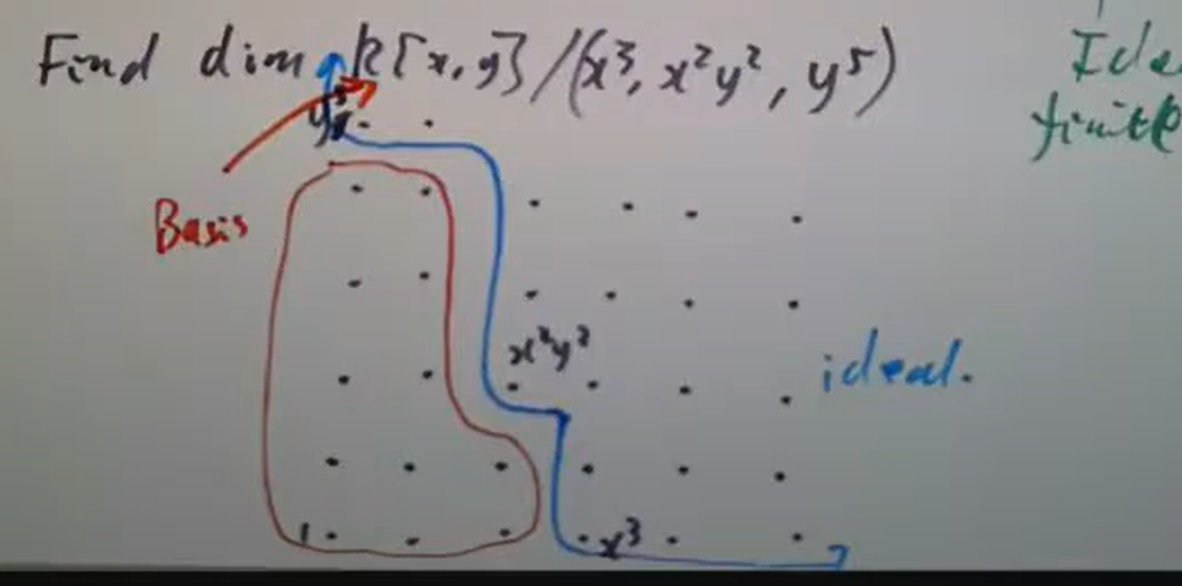 红圈中的元素便给出商环的一组基,于是立即可知 。
红圈中的元素便给出商环的一组基,于是立即可知 。
考虑二阶群作用于 ,把 打到 , 打到
,则它的不变量是某个多项式环上的自由模。这里画图证明不变量 上的自由模 注意到不变量环同构于 (其中
),于是我们也可以用上面的画图道理来研究例如圆锥 的结构等等。譬如说考虑 中的子式生成的理想,也就是
,注意到
而 ,令 ,则立即可知这是 被
作用的不变量(
是三次单位根),从而知 是 上自由模,且是整环,从而 是素理想。类似地通过画图我们也能知道
不是 上有限生成模
注意到不变量环同构于 (其中
),于是我们也可以用上面的画图道理来研究例如圆锥 的结构等等。譬如说考虑 中的子式生成的理想,也就是
,注意到
而 ,令 ,则立即可知这是 被
作用的不变量(
是三次单位根),从而知 是 上自由模,且是整环,从而 是素理想。类似地通过画图我们也能知道
不是 上有限生成模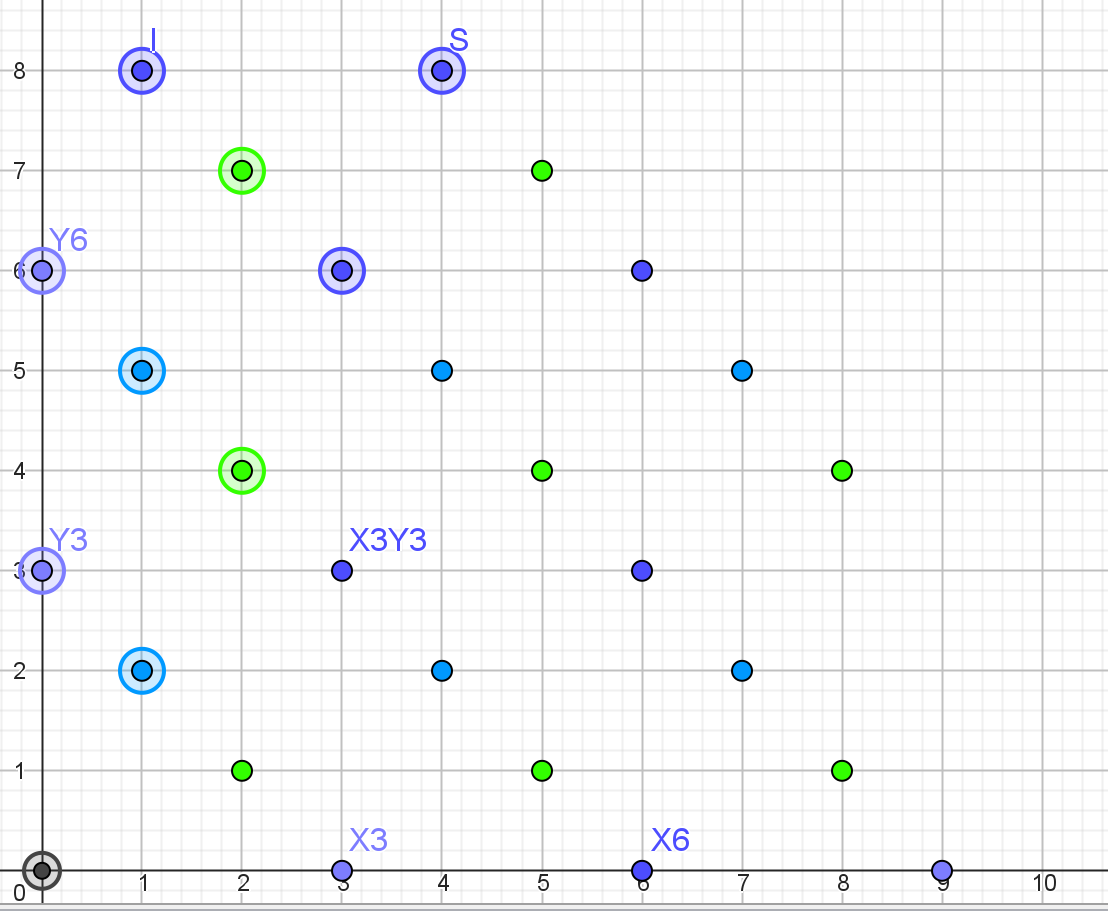
对形式幂级数环
,Weiestrass多项式是
中的首一多项式 ,其中 常数项为零(也就是不可逆)
(Weiestrass预备定理)
中任何形式幂级数可以唯一写作 ,其中, 是某个Weiestrass多项式, 是可逆元
只对
情形证明其中任何形式幂级数可以唯一写作
,多元情况的证明没区别。
假设 非零,把
因子提出来,那么不妨设系数非零的
中次数最小者为 ,则如图所示,给 乘上某个 可以消去 项,再乘某个 可以消去 项……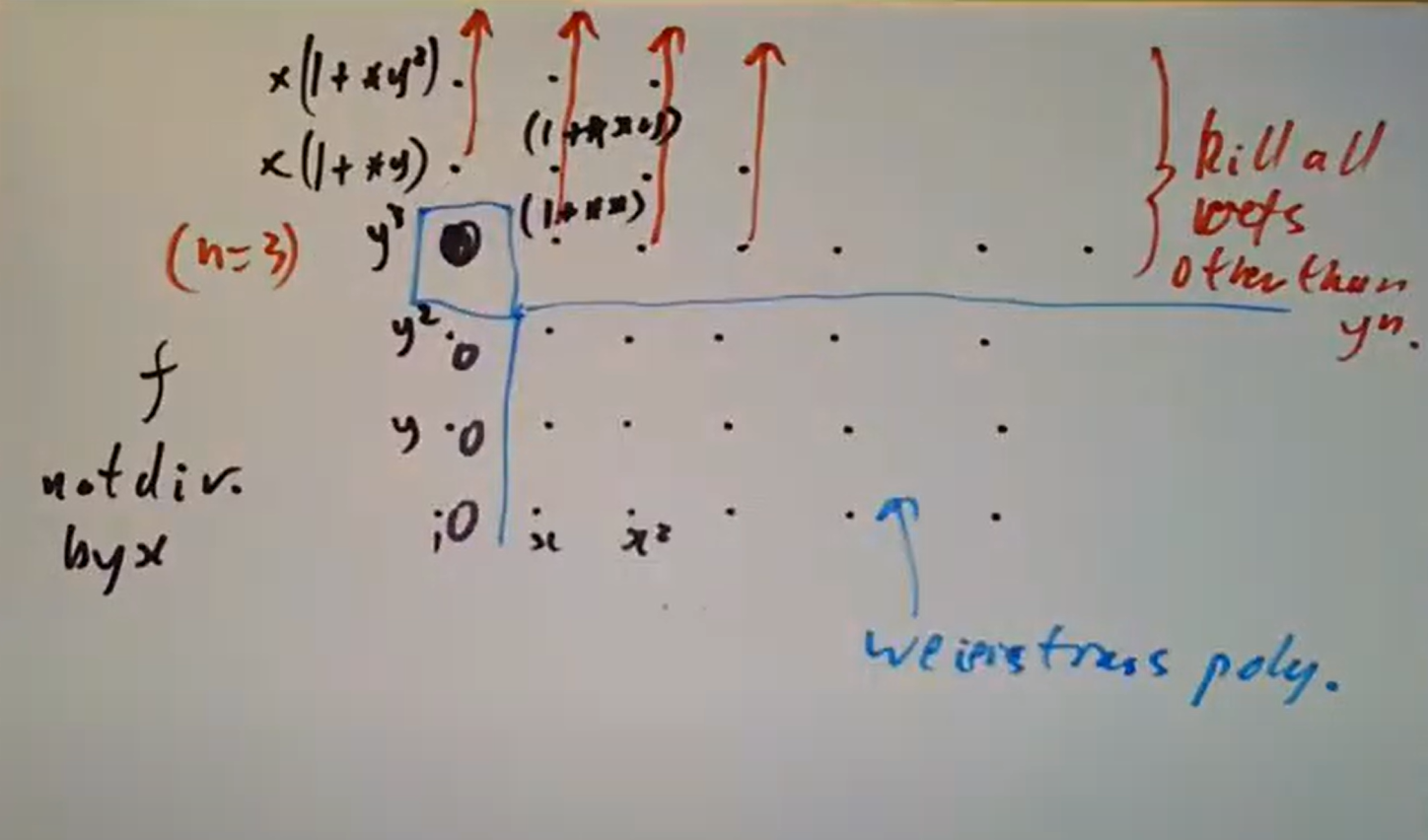 这样下来乘上这些元素的无穷乘积即可消去诸 ( ),进而类似地乘 消去
,……把这些乘积再乘起来得到某个可逆元,作用于
则得到Weiestrass多项式。从这样证明中其实也立即可见如此分解的唯一性。
这样下来乘上这些元素的无穷乘积即可消去诸 ( ),进而类似地乘 消去
,……把这些乘积再乘起来得到某个可逆元,作用于
则得到Weiestrass多项式。从这样证明中其实也立即可见如此分解的唯一性。
域上多元形式幂级数环是UFD
考虑二元情况。假设 不可约且
,想证明 或 之一成立,则只需考虑 是Weiestrass多项式的情形。现在 ,如果可以证明 是Weiestrass多项式,那么由 是UFD可以推出 或 。而想证明这点只需要考虑将 分解为 ,其中 是Weiestrass多项式,于是 给出 在 意义下的唯一分解,由是知
。多元情形与此并无区别,归纳即可。
注1:我们不能希望像 UFD推
UFD那样证明形式幂级数环UFD,因为
UFD不意味着 UFD,例如
是UFD( 在
的局部化)但其形式幂级数环不然。
注2:收敛幂级数环并非UFD。例如考虑一个有无穷多零点 的收敛幂级数 ,那么 皆整除 ……
环素谱的可视化
Exercises: 1.24
引入素谱的动机从一类特殊的环说起。对紧Hausdorff空间 ,考虑 (即 连续函数环),它是一个交换
-代数。 的极大理想和 中的点有着一一对应, 对应极大理想
。类似地也可以通过这样的办法来重建 的拓扑。
具体来说,首先证明 中素理想
中函数公共零点存在且唯一,从而极大理想自然具有
形式。如果不存在,那么对每个
都存在 ,从而在
某个开邻域非零,那么由紧性可以取出有限个 使对应开邻域覆盖 ,从而
为可逆元,矛盾。而若
是公共零点, ,那么取 的不交开邻域 ,由Urysohn引理存在 在 取 ,在 取 ,和 在 取 ,在 取 ,则 意味着 之一属于 ,可知 属于 从而 并非公共零点。
这种漂亮的对应我们希望也能推广到任意环上,于是得到了所谓环的极大谱,但有一个问题是极大谱不具有函子性(极大理想的原像不一定是极大理想,如
)。不过考虑到 的极大理想对应
满射的核,
复合不一定能确保满射,只能保证像
的子环,也就是像是整环,所以应该把极大理想修改为素理想,而且这样确实可以处理这一问题。于是我们便得到了素谱:
环
的素谱 定义为 全体素理想组成的集合,配备由 定义闭集所给出的拓扑,其中 为全体包含理想
的素理想组成的集合。具体的验证和一些性质见Atiyah第一章习题。
零环的素谱是空集; 由单点组成。
中极大理想的拓扑和
的拓扑完全相同。事实上考虑 子集
的闭包对应
中的极大理想,证明同样Urysohn秒杀之。
的素理想里面极大的部分形如
,其中
,而唯一的非极大素理想是
,它在拓扑上是一个“一般点”(generic
point),闭包是全空间。可视化的话就可以画成如图中的样子,不过全体闭集是全集和一切有限集,蓝色的是一般点

考虑
,其中极大理想是
,非极大理想是 ,闭集是 的有限子集或
,它可以被可视化为这样的形象,其中
是一个“一维的”一般点,而诸极大理想落在其闭包上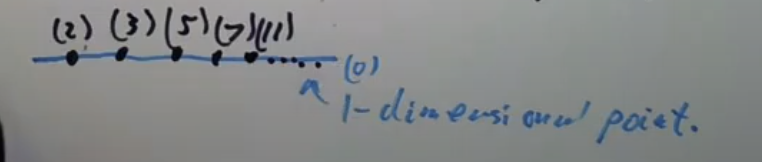
中,极大理想是
和
,非极大理想依然是一般点 ,某种意义上可以看作“对折”的 。更一般地来说, 是 加上 作用于 的轨道,其中 为
的代数闭包。
令
, ,则 便是 的特征值(考虑到 ,从而非零素理想都形如 ),而特征值被称作谱是由于量子力学上的渊源,这也是为什么素谱被称作“spectrum”的原因之一。
某种意义上我们可以这样分解 
考虑
, 嵌入诱导出 ,从而给出这样的可视化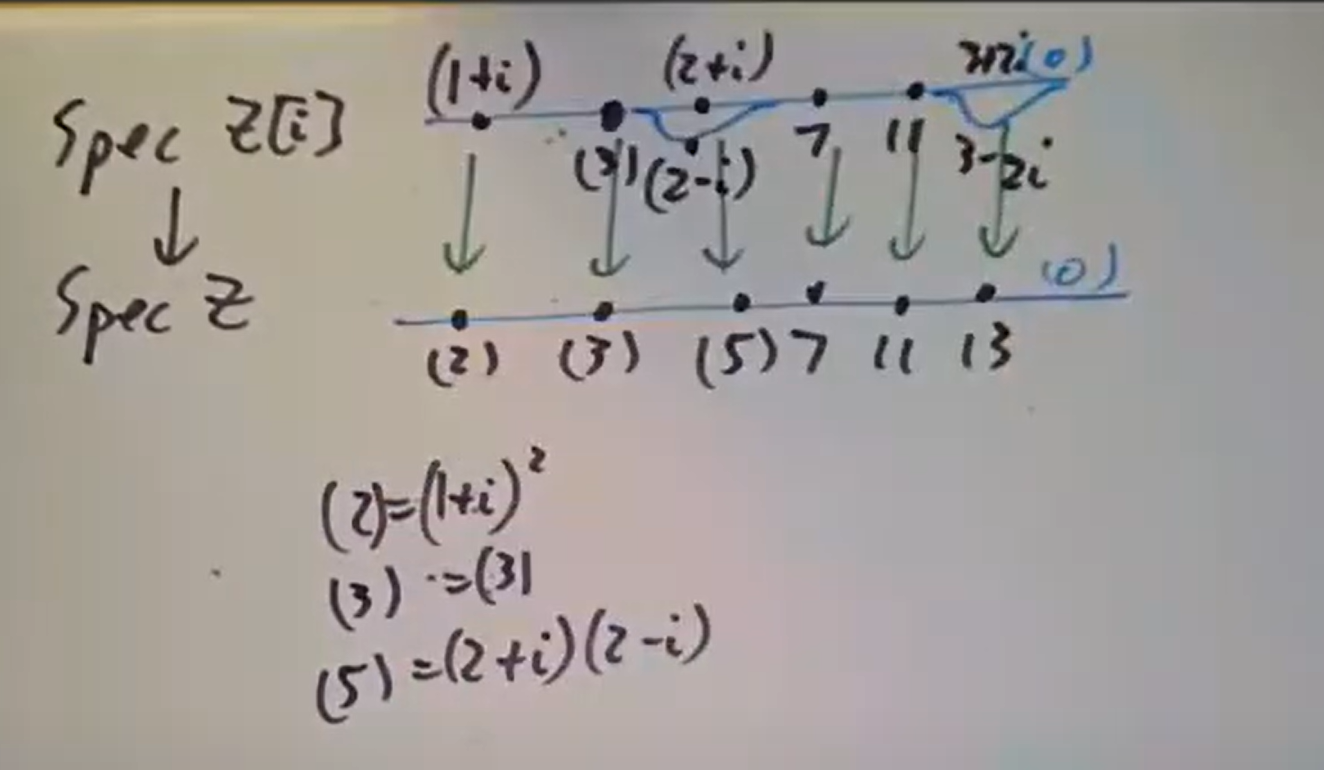
中,极大理想形如
对应单点,其它非零素理想形如
其中 是素元( 中互素多项式
只能有有限多个公共零点,从而对非主理想 , 是基数
的有限集(按零点定理如果它只有唯一公共零点,则具有 形式),从而可约,于是
非素理想),除此以外依然有一般点
,可视化如图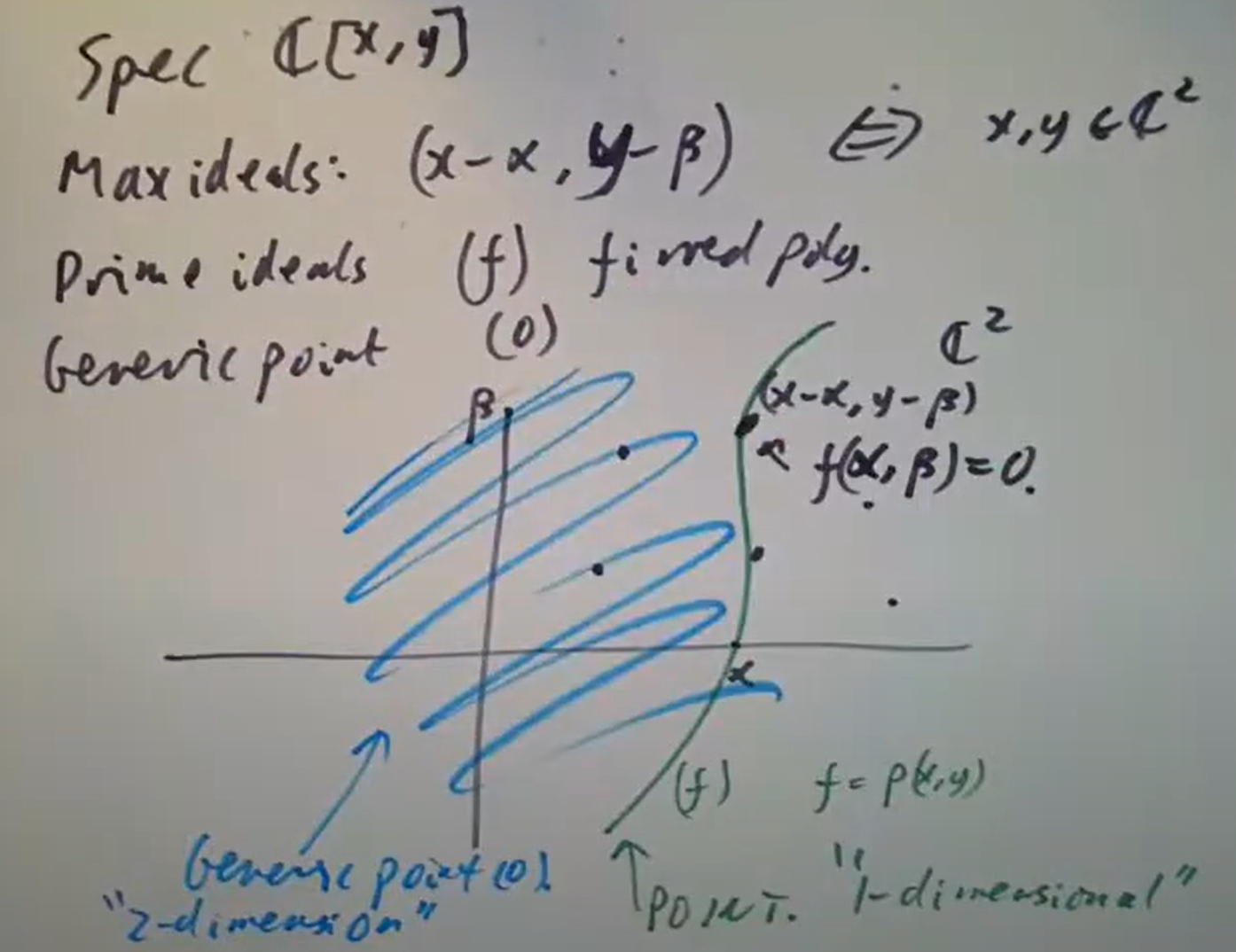
中,极大理想只有 (
元素皆可逆),而非极大素理想皆为主理想(考虑到 的分式域
,也就是全体 组成的形式幂级数域,假设素理想 非主,也就是存在互素 ,对 使用Weiestrass预备定理,则要么直接
在 中,要么不妨设 是Weiestrass多项式,但后一种情况下在
中存在环量组合为
,也就是 中存在 使 ,于是知 ,类似对 应用预备定理知 ,从而 ),形如 ,其中
不可约,某种意义上可以可视化为过原点的全体“无穷小”这样的
考虑
,首先由
得到 ,然后考虑这个映射的纤维: 的原像即为 中包含 的素理想,也即是 ,而对 的原像,考虑 中常数项平凡的素理想 ,则有 (考虑到 在 中生成的理想形如 ),
考虑模形式定义Hecke算子考虑
张成的Hecke代数,于是这个Hecke代数也可以视为
的子环,由一切 生成,而已知
,于是我们知道这个环 实际就是所有 ,其中 。通过 嵌入得到
,而考虑到 即
,于是有如下可视化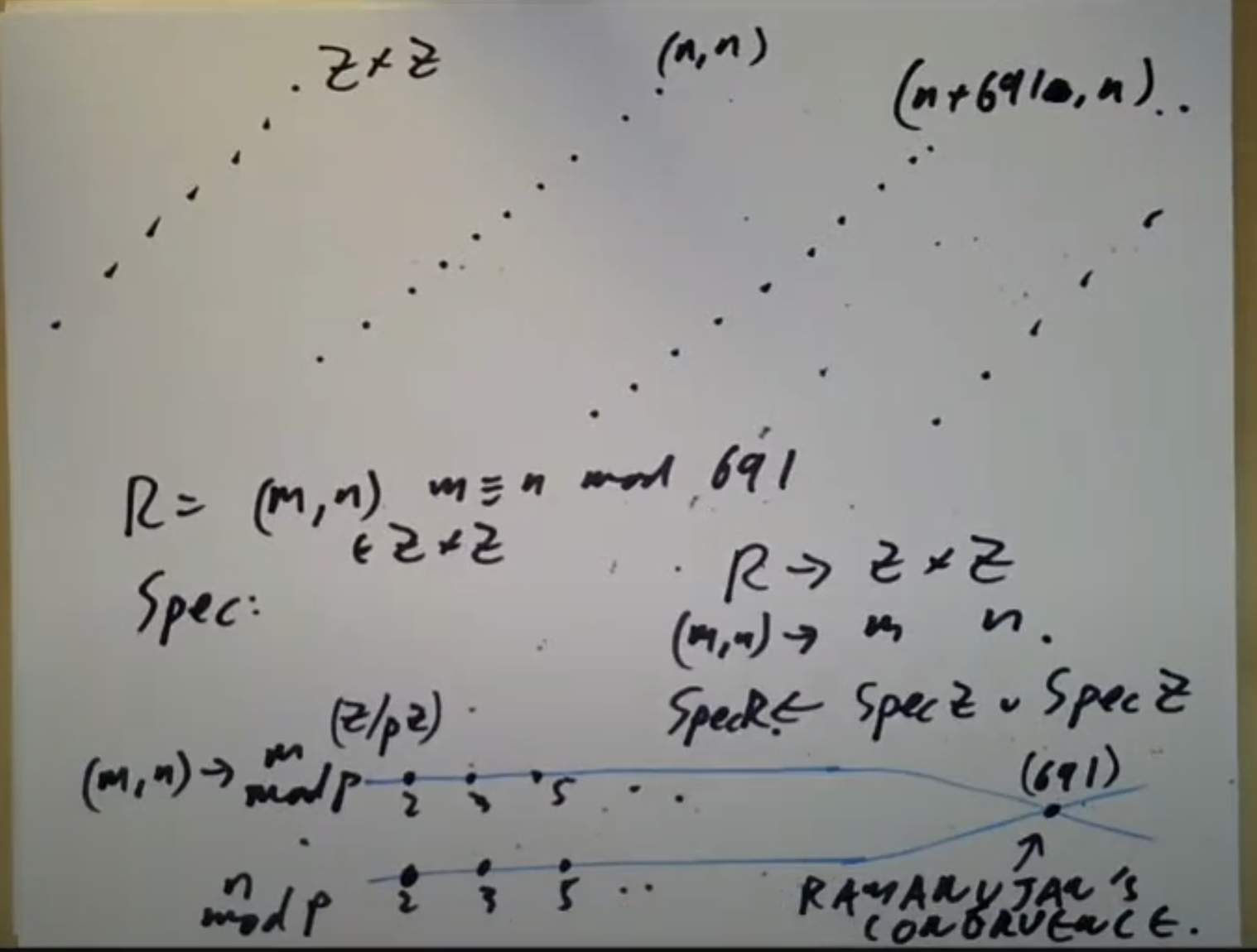 像691这样的素数被称为Eisenstein素数。
像691这样的素数被称为Eisenstein素数。
Exercises: 1.13, 1.14
Draw Spec R, where R is the subring of elements (m,n) of the product ZxZ
with m = n mod 100.
素谱的拓扑
环
的素谱 拟紧
被开集族
覆盖相当于说不存在某个素(极大)理想包含一切 ,也就是诸 生成的理想是 ,其中有限多 环量组合出 。
注:拟紧和紧的定义完全一致,叫这个名字只是因为20世纪50年代拟紧被定义时,紧经常指紧Hausdorff。
,而后三个环都只有一个素理想,因而 形如
令
为Klein四元群,考虑
。假设 为 的特征,也就是 中同态,则
是幂等元。具体到 , 由四个元素 组成,其中 且 ,从而易知 有四个特征,于是得到四个幂等元满足 , 且 ,于是从而可以可视化为
Exercises: 1.10, 2.25
Draw Spec Z[Z/6Z] = Z[x]/(x6-1), the group ring of the cyclic
group of order 6.
不可约空间
称拓扑空间
不可约,如果
非空且不是两个真闭子集的并,或者等价来说 中任意两个非空开集有交
不可约是极强的性质,而且高度非Hausdorff,事实上Hausdorff且不可约等于说
是单点。
,从而不可约。
令
为Klein四元群,
是一个非不可约空间的例子。事实上 嵌入,以及
的四个特征给出素谱间的反向连续映射。事实上考虑 的纤维,其中 包含素数 的素理想
一一对应于 的素理想,而 到域的同态像特征 ,从而只能是 或 ,由是知 时, 的素理想对应 的四个特征,而不包含任何素数的情形就是
的例子。接着考虑
的四个映射,便得到可视化 总共这里有四个不可约分支,对应四个 中点的闭包
总共这里有四个不可约分支,对应四个 中点的闭包
形如 轴和 轴之和,这是两个不可约分支(irreducible
component)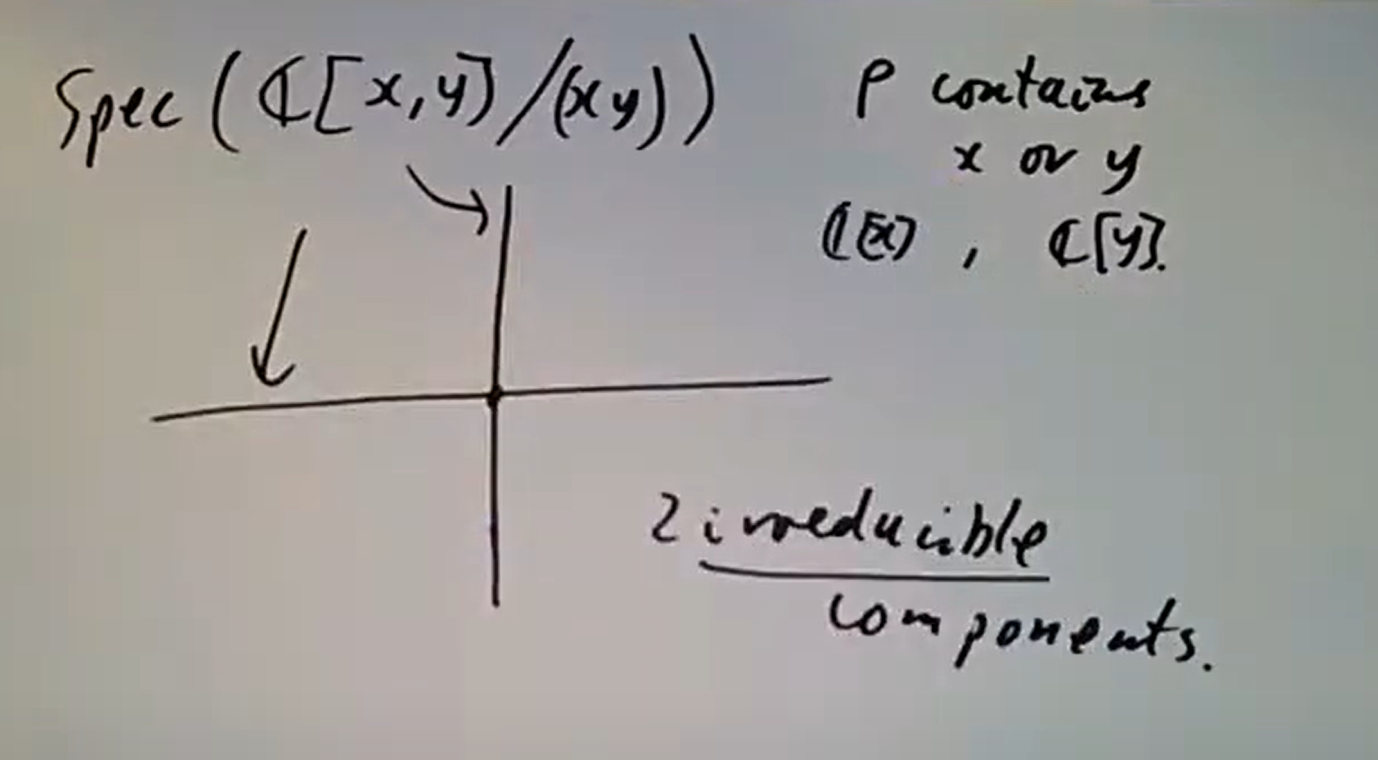
不可约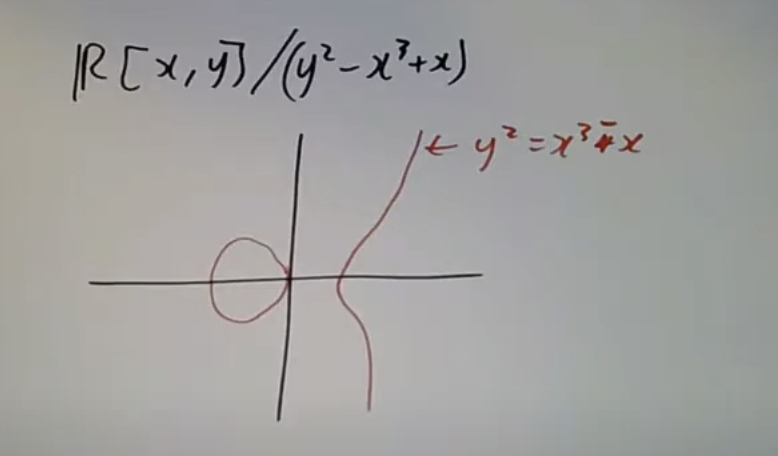
假设
是环 的乘性子集, 是与 不交的理想,则存在素理想包含 且与 不交
对全体包含 且与 不交的集合应用Zorn引理得到某个极大元
,假设 ,则 和 不能都与 有交,不妨假设是 ,从而由极大性 。
中,某个闭集不可约当且仅当其具有 形式
事实上假设
不可约,那么不妨设 ,现证
是素理想。事实上对 , 意味着 ,则由不可约应有
或 ,不妨设 ,那么假若 ,则 与 不交,应用引理得到素理想 包含 且与 不交,与 矛盾。
对紧Hausdorff空间 ,考虑 (即 连续函数环)的素谱。首先
中极大理想具有
形式。假设 为 的素理想,则
中函数公共零点存在且唯一,从而包含于唯一的 。此外可以证明,如果 是闭的素理想,则 。
但非闭的素理想则会变得奇异。考虑如此构造:取某个非孤立点 ,则可以找到 使得 且 在 的任何邻域上不恒为零,于是取 为某个在 某个邻域上为 汉斯组成的理想, ,依 存在素理想 包含 而与 不交,所以 真包含于
,于是是非极大的素理想。而且商掉非闭的素理想会导致商环本身拓扑非Hausdorff,这是很糟糕的性质。
Exercises: 1.9, 1.11, 1.25
诺特空间
拓扑空间
诺特,如果下列等价条件成立:
(i) 非空闭集族有极小元
(ii) 非空开集族有极大元
(iii) 开集无穷包含升链稳定(闭集包含降链同理)
(iv) 开集(事实上任何子集)皆拟紧
诺特环 的素谱
是诺特空间
考虑到
中闭集皆形如 和 中的(i)。
令
,则 只有唯一的素理想 ,此理想非有限生成,故
非诺特,但
是单点从而诺特。这说明
的逆命题并不成立。
Hausdorff和诺特是高度不相容的性质。
若Hausdorff空间 诺特,则
是有限集的离散拓扑
只需证
有限,有限Hausdorff自动离散。取 ,对任意 ,取不交开集 分离 与 ,其中 ,则依 紧性,可以取出有限多
覆盖 ,而对应 的交 是开集。
(Noetherian induction)假设
是诺特空间, 是关于 的闭集的性质,则如果对任意闭集 , 的任何子集具有 蕴含 ,则 的任何子集都具有
取所有不满足
的闭集组成集合,如果非空则取极小元即得矛盾。
诺特空间中的闭集皆为有限多不可约闭集的并
令 为“ 是有限多不可约闭集的并”,则闭集
要么本身不可约,要么是有限多真子闭集的并,故可以应用诺特归纳。
与
结合某种意义上就分类了诺特环素谱的全部闭集。
为紧Hausdorff空间, 并非诺特环,考虑 。
中不可约闭集形如
,所以如
中所述,至多包含一个极大理想,因此
中显然会有巨量闭集不能被表示为有限多不可约闭集之并(譬如说考虑到
中极大理想重建了 的拓扑,见 ),是一个高度非诺特的空间。
令
为 的中心,也就是
, ,
生成的环(有限群的话只取决于共轭类),作为Abel群 ,而且现在我们想研究
和其中的不可约元素。
取 中素理想 ,则 中 ,即 或 。带入上面其它约束条件知 时得到 ,而 时 ,这给出了 三种可能的同态(事实上 ),诱导出三个同态 。
现在考虑 的纤维,和 时完全相同,包含素数 的理想对应 系数的情形,而模 或 时, 同态和 同态相同,而 同态只在模 时与前两者相同,于是有如下可视化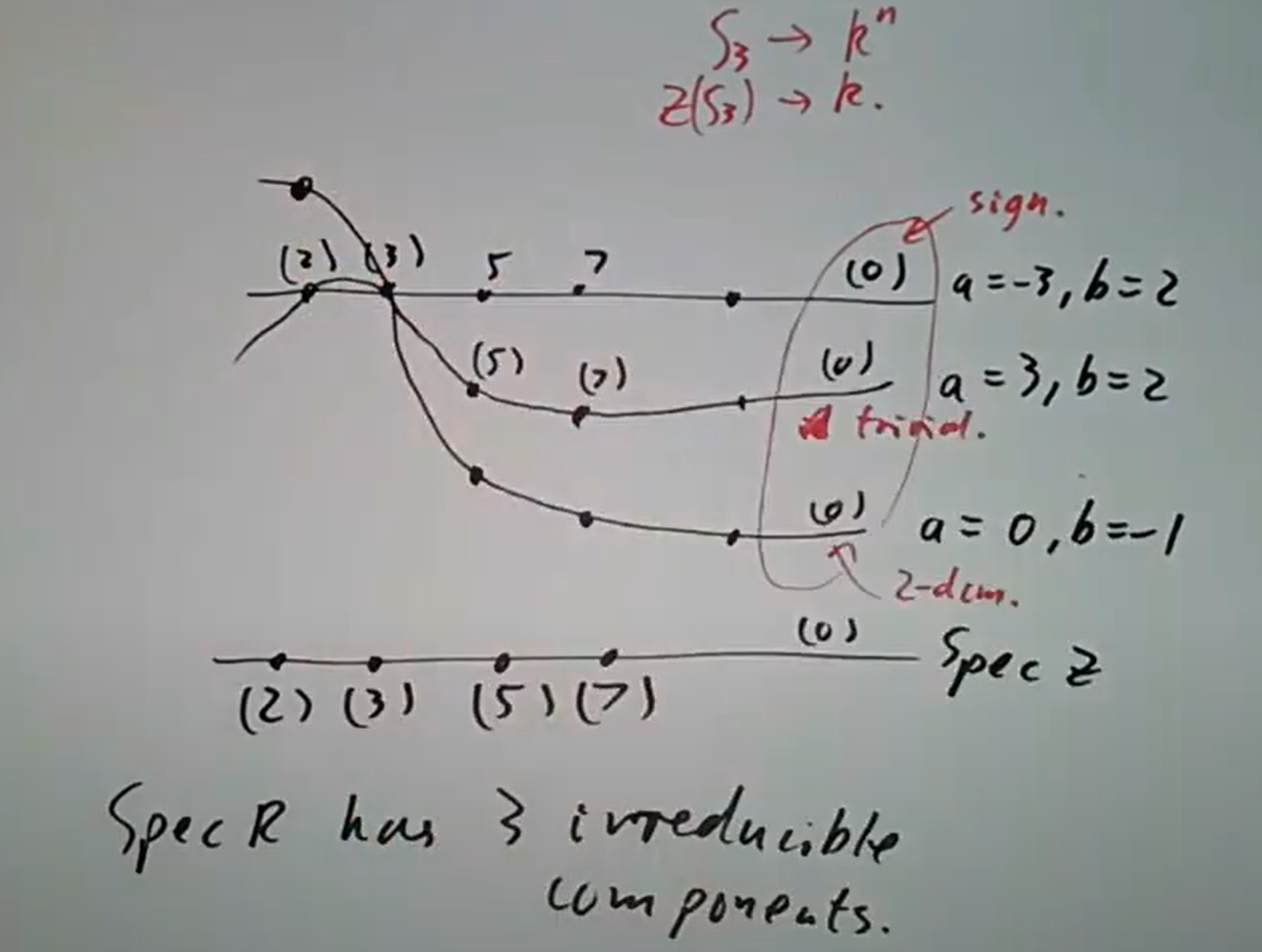 三个不可约分支对应三个 的闭包。由此也可以得到
的全部不可约闭子集,无非是图上某个点的闭包。这和
的表示密切相关,这三条线某种意义上和
的三个不可约表示有对应,具体的对应关系图中已经标注。图中除了 或 的其它素数处和 处并无本质区别,某种意义上这是因为
的表示论在特征非 或 的域上和特征 情形区别不大,而特征为 或 时则会出现奇异的性质,这与 的modular representation
theory很有关系。
三个不可约分支对应三个 的闭包。由此也可以得到
的全部不可约闭子集,无非是图上某个点的闭包。这和
的表示密切相关,这三条线某种意义上和
的三个不可约表示有对应,具体的对应关系图中已经标注。图中除了 或 的其它素数处和 处并无本质区别,某种意义上这是因为
的表示论在特征非 或 的域上和特征 情形区别不大,而特征为 或 时则会出现奇异的性质,这与 的modular representation
theory很有关系。
Exercises: 1.2
 此外有高斯整数
此外有高斯整数  这种可视化手段的一个直接应用是:
这种可视化手段的一个直接应用是: 则立即可知上述
则立即可知上述 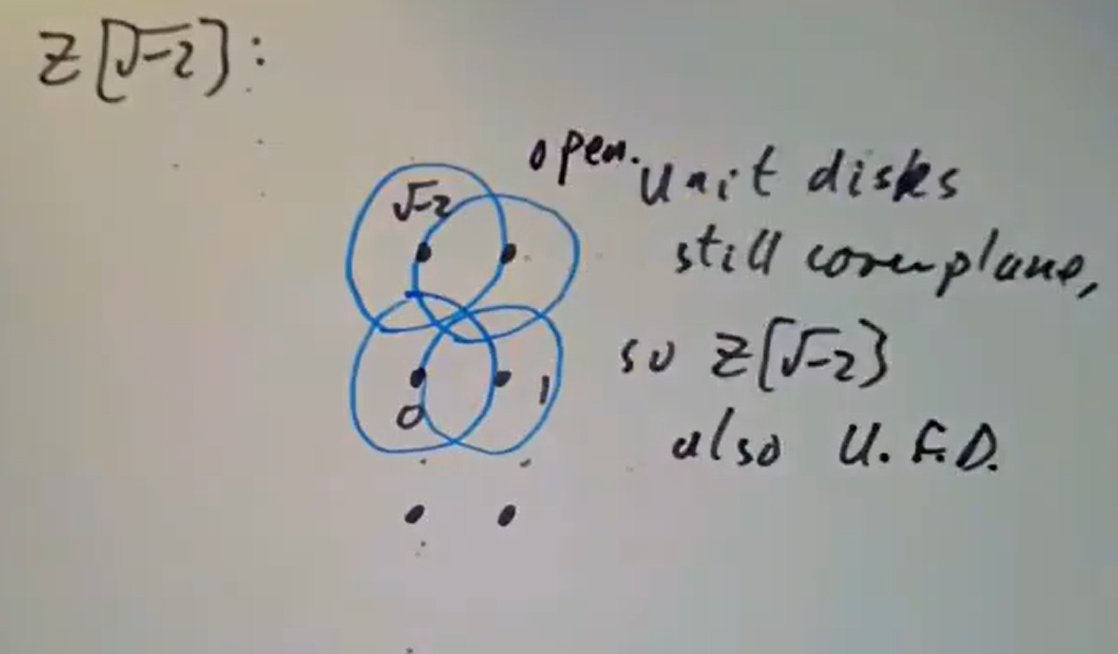 画图立即可知。
画图立即可知。 非但如此,
非但如此, 这里
这里 
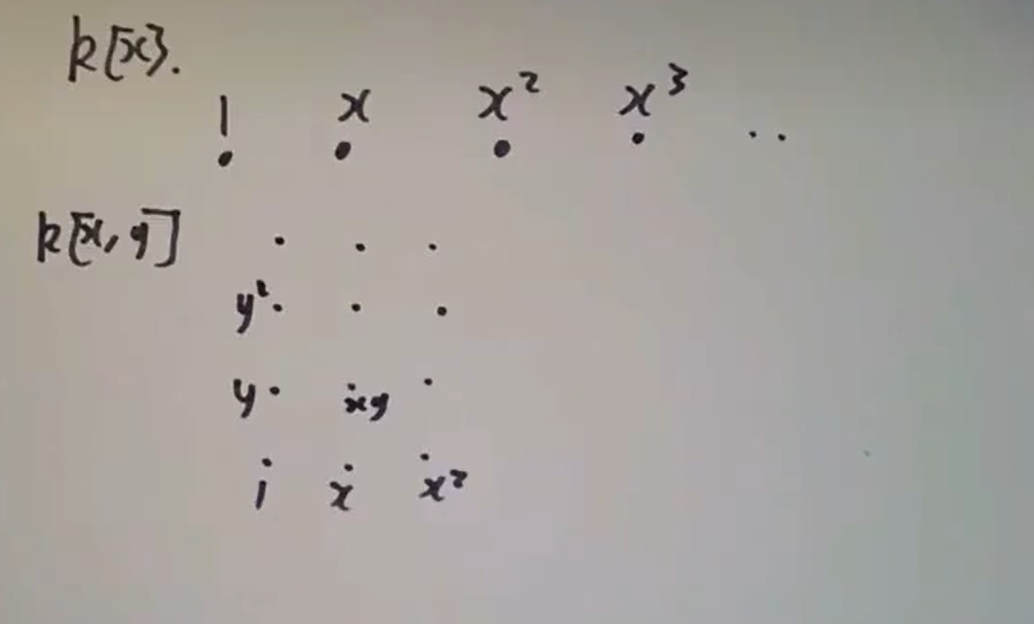
 红圈中的元素便给出商环的一组基,于是立即可知
红圈中的元素便给出商环的一组基,于是立即可知  注意到不变量环同构于
注意到不变量环同构于 
 这样下来乘上这些元素的无穷乘积即可消去诸
这样下来乘上这些元素的无穷乘积即可消去诸 





 像691这样的素数被称为Eisenstein素数。
像691这样的素数被称为Eisenstein素数。

 总共这里有四个不可约分支,对应四个
总共这里有四个不可约分支,对应四个 
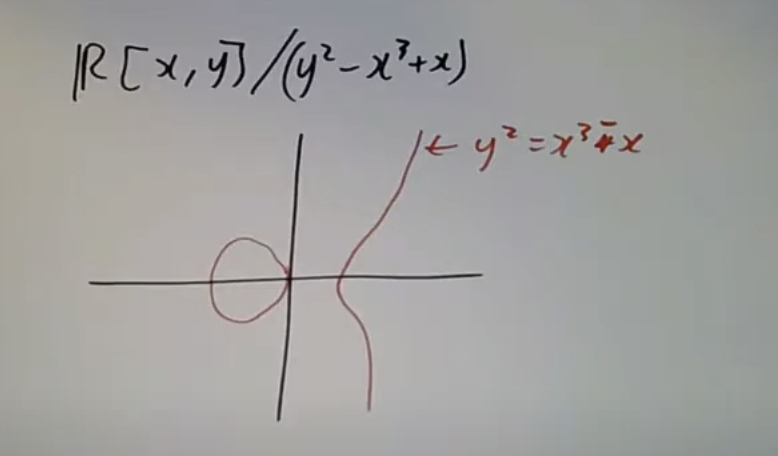
 三个不可约分支对应三个
三个不可约分支对应三个