Notes on Serre's Finite Group 2
(b)
Notes on Atiyah's Commutative Algebra 7
对
这涉及到无穷多次求和的操作,但注意到其中
Notes on Neukirch's Algebraic Number Theory 1
Notes on Galois Theory
Emil Artin之Algebra with Galois Theory中Ch5的省流版。以及Borcherds的Galois Theory课的部分内容
分裂域与代数闭包
设 ,则存在域扩张 使 在 上分裂
在
5.1中得到的扩域是最小的使 分裂的扩域
任何
假设 与 同构, 对应于 ,假若 分别是 分裂域,则 和 同构可以延拓至 同构,特别的, 在 上分裂域在同构意义下唯一
素因子分解
对域 ,存在 的代数扩域 ,使得 代数闭,把 称为 的代数闭包
考虑
现在假设
注:代数闭包在同构意义下唯一,但并不具有函子性(比如说事实上考虑它的构造依赖选择公理),以及绝对Galois群
一种绕过这组问题的手段是考虑Groupoids(态射皆iso的范畴),我们有
有限域
有限域 是 的分裂域,其中 , 阶有限域在同构意义下唯一
找到有限域上不可约多项式的一个有效算法是筛法,和整数情况并无区别,比如说我们可以找到
我们可能很想要一个“标准的”多项式取法,让我们可以比较典范地把
当且仅当
事实上考虑
作为一个应用,我们可以计算
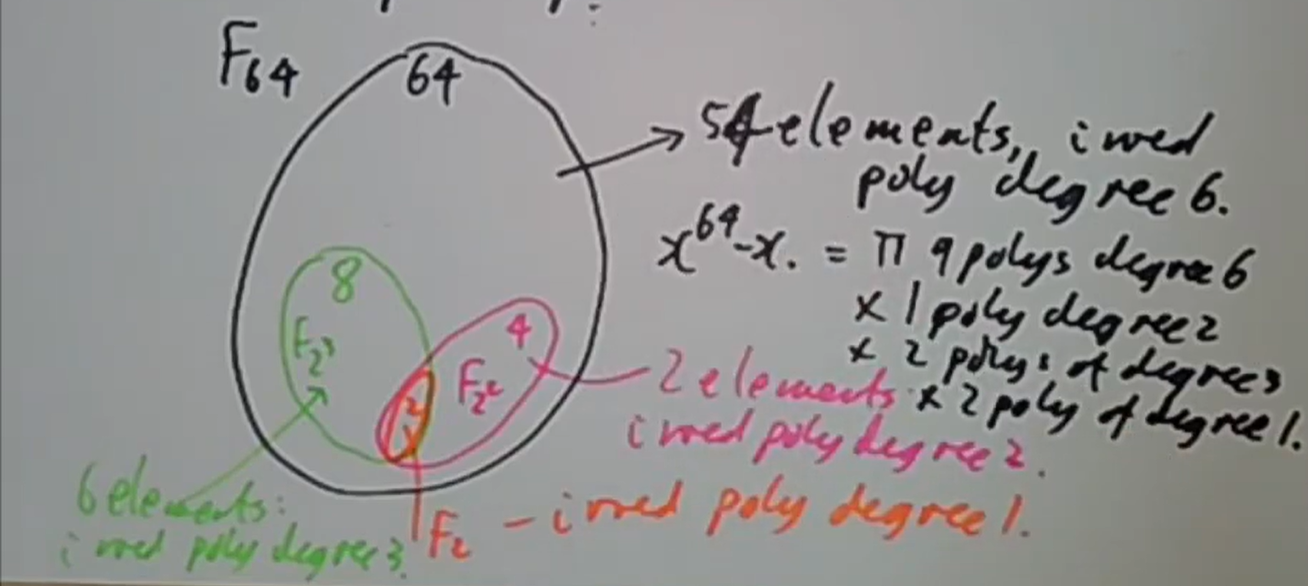 作为结果我们知道
作为结果我们知道
可分扩张
假设
在 上有素因子分解 诸 非线性,如果 在 分裂域 中皆无重根,则 中没有 以外的元素在 作用下不动
事实上只需证明,对代数扩张
接着对
特征 域上不可约多项式无重根(也就是可分),特征 上不可约多项式则会分裂为 形式
如果不可约多项式
有限域的代数扩张皆可分
只需考虑有限扩张,
假设 是代数扩张,设 是 的可分闭包(即所有 中可分元组成的域),则 是可分扩张,而 是纯不可分扩张,也就是 中所有元素都是某个 的根,这里
Galois理论的主要关注点就在于可分扩张的部分。
正规扩张
一般来说正规扩张的正规扩张未必正规,例如
群 在 中的不同特征(即 中非零元) 线性无关,特别的, 的不同自同构作为乘法群的特征 -线性无关
假设诸
假设 是由 的自同构组成的群 中元素, 是 的不动域,则
只需证对
现在考虑以上方程被
现在只需要找到合适的
是 -自同构 组成的群, 是 的不动域,则 是可分正规扩张
取
事实上
有限扩张 是正规扩张当且仅当 是 上某个可分多项式的分裂域
事实上我们有
设 是代数扩张,则以下条件等价:(1) 正规 (2)如果 中不可约多项式 在 中有根,则 在 中分裂 (3) 是 上某个可分多项式族的分裂域 (4) 取 的代数闭包 ,对 ,对任意 ,
(2)
(3)
(4)
Galois理论基本定理
设 是有限扩域, ,以下条件互相等价(满足其一者称为Galois扩张):(1) 是正规可分扩张 (2) (3) (4) 是某个可分多项式的分裂域
(1)
(2)
(3)
(4)
(Galois Corresponding)有限扩张 Galois当且仅当任何中间域 和子群 有反序的互逆双射
假设  现在我们想证明这两个包含关系取到相等,只需证明它们具有相同大小(对域指index,而群指阶数)。
现在我们想证明这两个包含关系取到相等,只需证明它们具有相同大小(对域指index,而群指阶数)。
我们将证明命题中的两个映射都保持“大小”,从而我们想证明的两个包含关系两端大小相同。具体来说,我们将证明
现证
注:如果没有


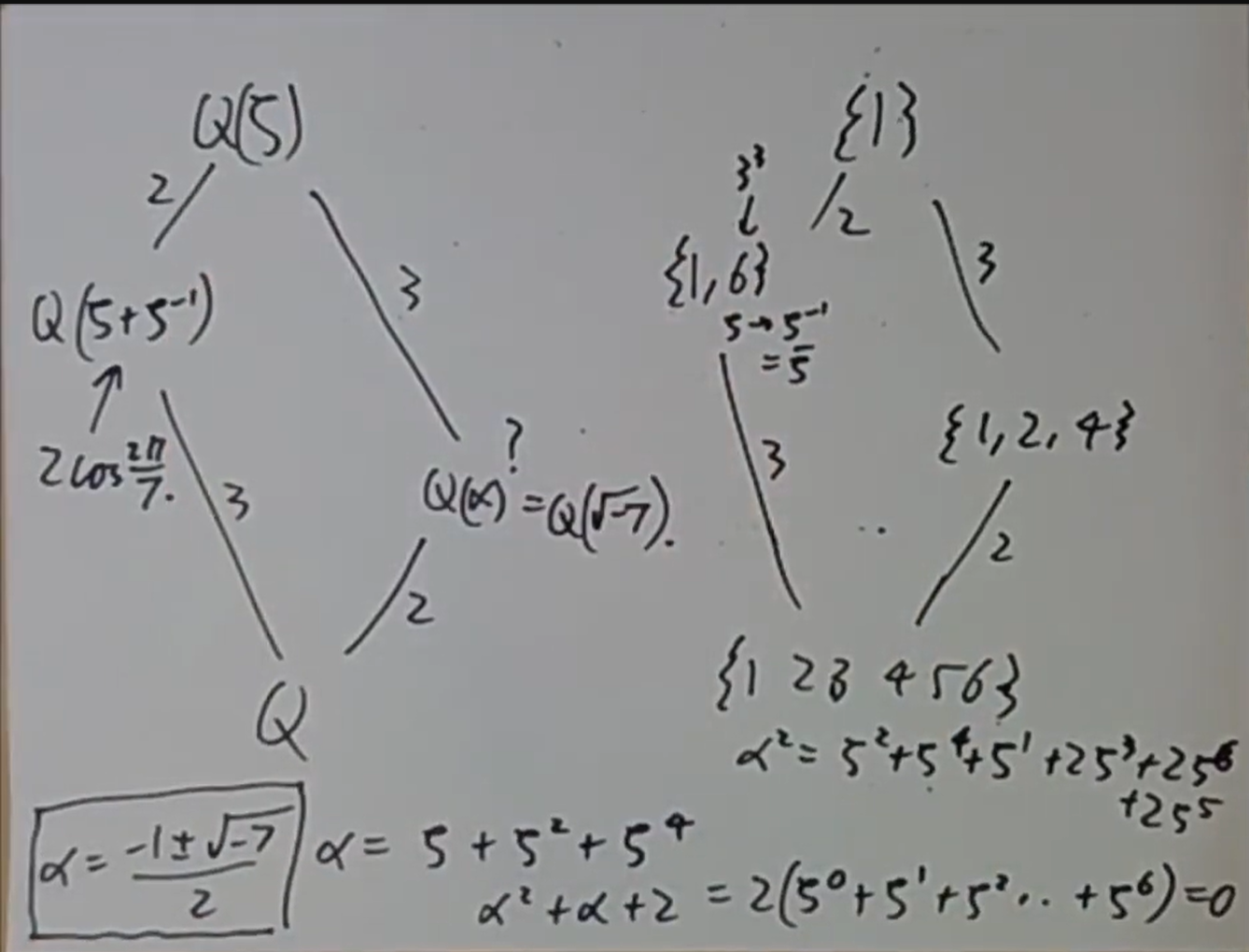 由此我们可以反求出它对应的子域。对三次的子扩张,它在
由此我们可以反求出它对应的子域。对三次的子扩张,它在
 则立即知
则立即知
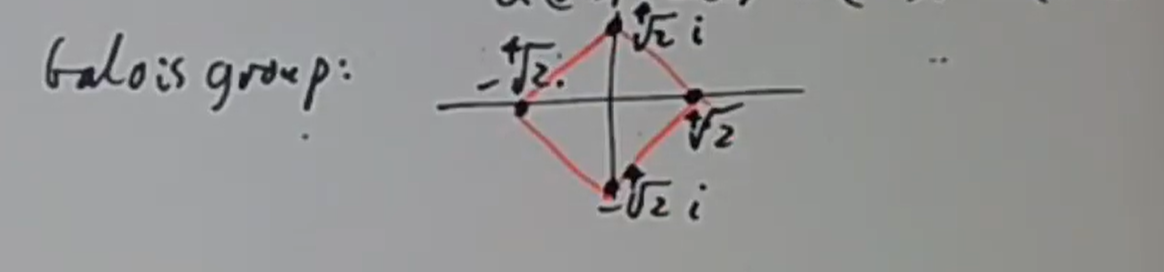 由于
由于
也可以可视化如图,上面五个二阶群中绿线是对称,中间的是旋转180度,下面的则是矩形的对称群和正方形的旋转群
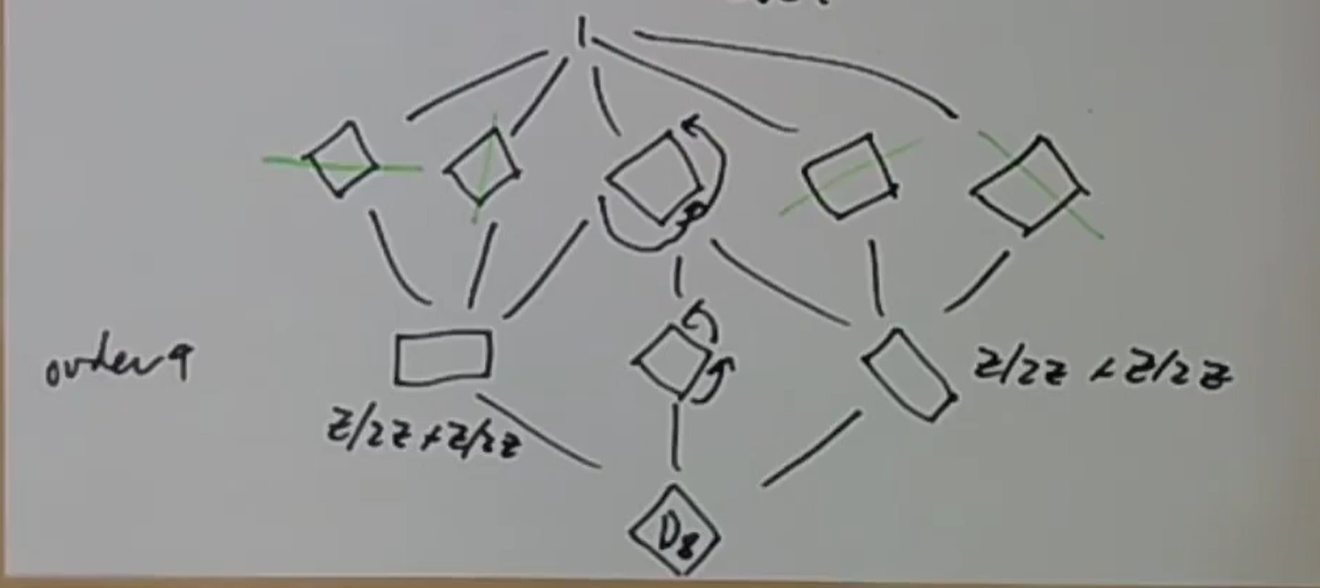 通过这些Galois群可以很容易地计算出对应的不动域
通过这些Galois群可以很容易地计算出对应的不动域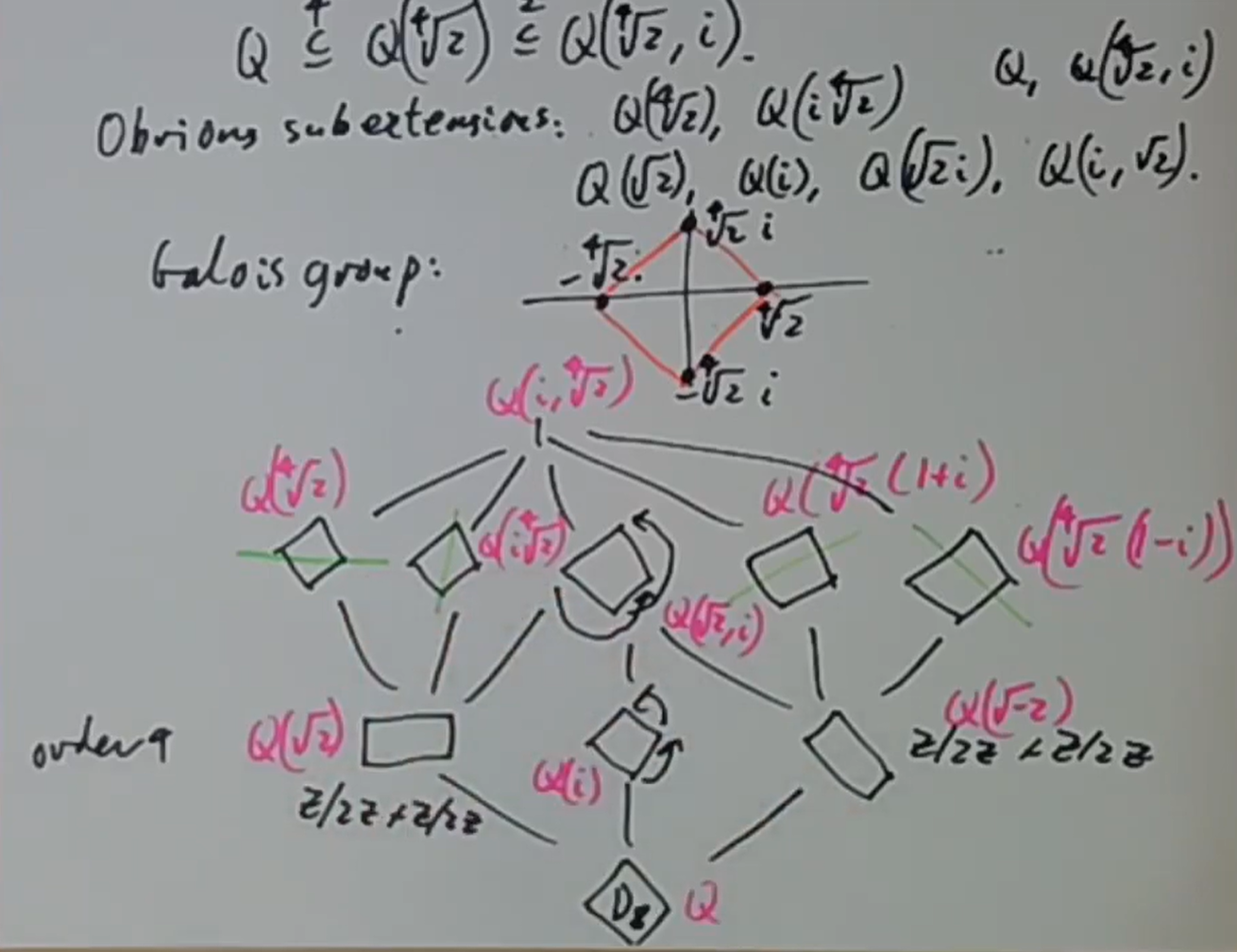 具体来说,由于
具体来说,由于 这里左边的两个对称和右边的两个对称分别互相共轭(从而不动域也共轭),除了这四个子扩张,剩下的子扩张皆正规。
Notes on Atiyah's Commutative Algebra 6
对Artin环情形此结论不成立,本章开头例子里(3)中Artin非诺特环就是反例。显然
Notes on Commutative Algebra 5
Artin模
Reading: Section 2.4
Exercises: 2.23
Classify the modules of finite length over k[x]. Find an Artinian module over this ring that is not Noetherian.
单模是非零的,子模只有 和它自己的模
环 上的单模有且仅有 , 是 的极大理想
对模 ,称它的一个合成列是子模的链 且每个 皆为单模,如果 有合成列则称 有有限的长度
长度有限当且仅当 既Noether又Artin
假设
反过来,可以不断选取
下面这个定理属于带算子的群上Jordan-Holder定理在关于模的情形:
如果 长度有限,则 的合成列都有相同的长度,且每个单模在合成列中出现的次数与合成列的选取无关
取两个合成列  其中
其中  现在考虑按图中最右上和最左下两个路线得到的合成列就是
现在考虑按图中最右上和最左下两个路线得到的合成列就是
假设有正合列 ,如果 长度有限,则 长度有限,且长度等于 与 的长度之和
Artin环
Reading: Section 2.4
Exercises: 2.6, 2.22 (this one is a bit tricky)
某种意义上Artin环是有限维线性空间的推广。
下列条件等价:
(i)诺特且 是极大理想的乘积
(ii)诺特且素理想皆极大(也就是 零维)
(iii)长度有限
(iv)是Artin环
(i)
(ii)
(iii)
(iv)
现在证明
注:
Artin环只有有限多极大理想,且是Artin局部环的乘积
考虑
Artin环的素谱是有限集的离散拓扑,极大理想给出其中的所有点
注:若诺特环的
Artin环皆长度有限,所以可以按照长度来分类。长度
长度
Reading: Section 2.4
Exercises: 2.24
Try to classify Artinian rings of length 3 or 4 over a field. (You do not need to succeed: the point is that you see how complicated this is.)
Notes on Commutative Algebra 3
局部化的定义
直观上,
这种形式上取逆的做法事实上比较非构造性,让我们对
直接考虑将
更进一步的,对于
于是
Reading: Section 2.1
Exercises: 2.1, 2.7
局部化的
注意到若
某种意义上可以将  事实上
事实上
首先
一般来说
 注意素理想局部化的素谱和商环的素谱大相径庭,譬如说
注意素理想局部化的素谱和商环的素谱大相径庭,譬如说
一般来讲,
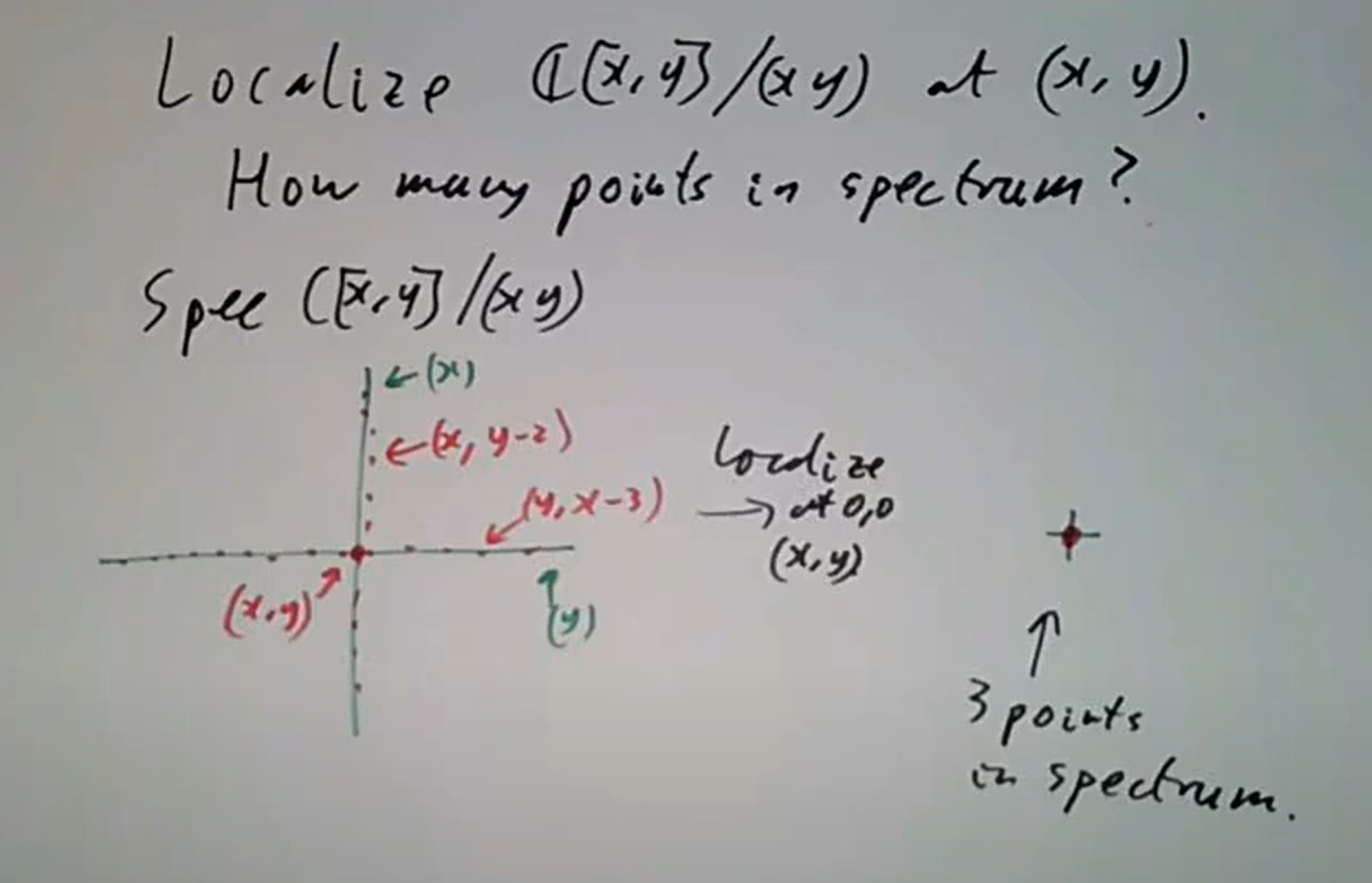
Reading: Section 2.1
Exercises: 2.10
对紧Hausdorff空间
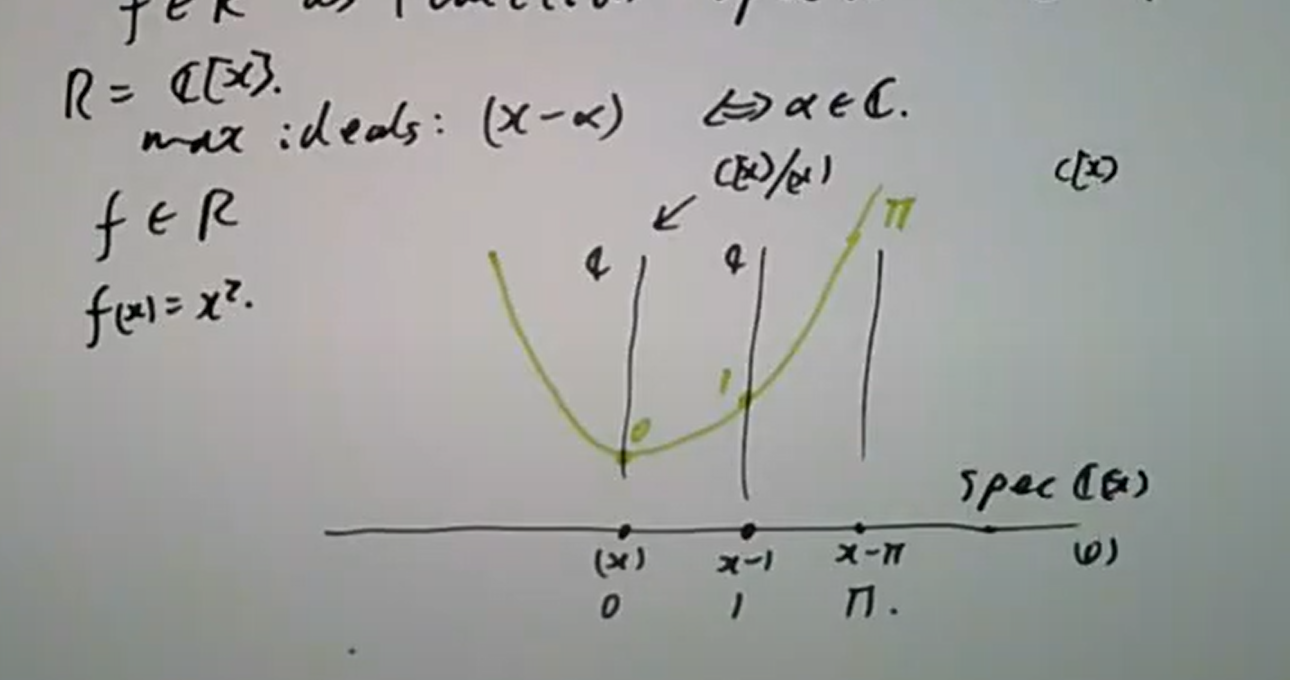
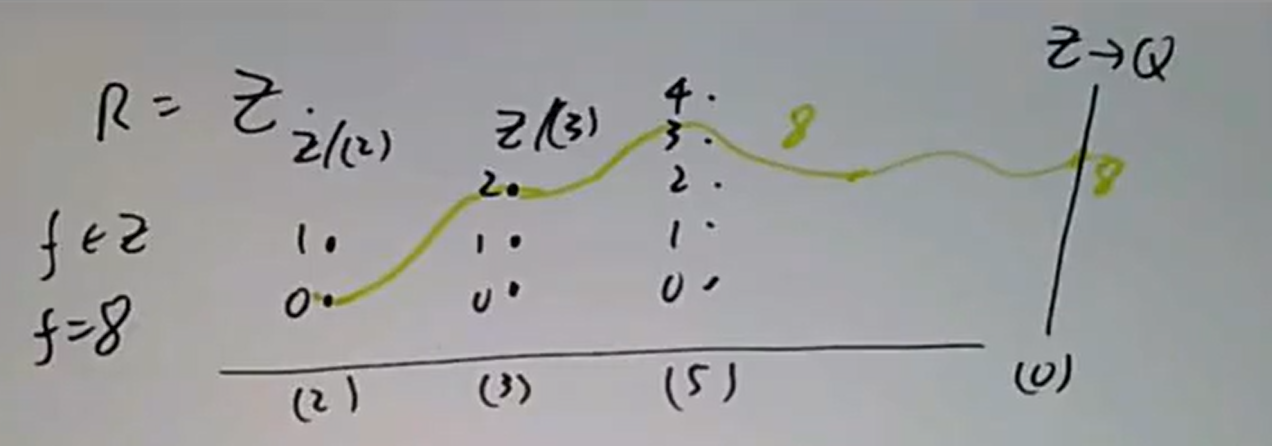
但这种函数化会出现一个问题,就是
事实上我们有更好的方法来表示出这样的函数,具体来说是使
(i):如果
(ii)(预层性质):如果
(iii)(层性质): 如果
我们希望对任意的环
直观上来说,
Exercise: 2.6
Exercises: Suppose R is the ring of continuous real functions on the circle. Is the natural map from R to the localization at a maximal ideal injective? What if R is the ring of smooth functions on the circle? What if R is the ring of analytic functions on the circle?
仿射概形
某种意义上仿射概形的观点在于将
具体来说 (1) 对含入映射(对应函数的限制)
假设
这里只考虑

下面是一些基本例子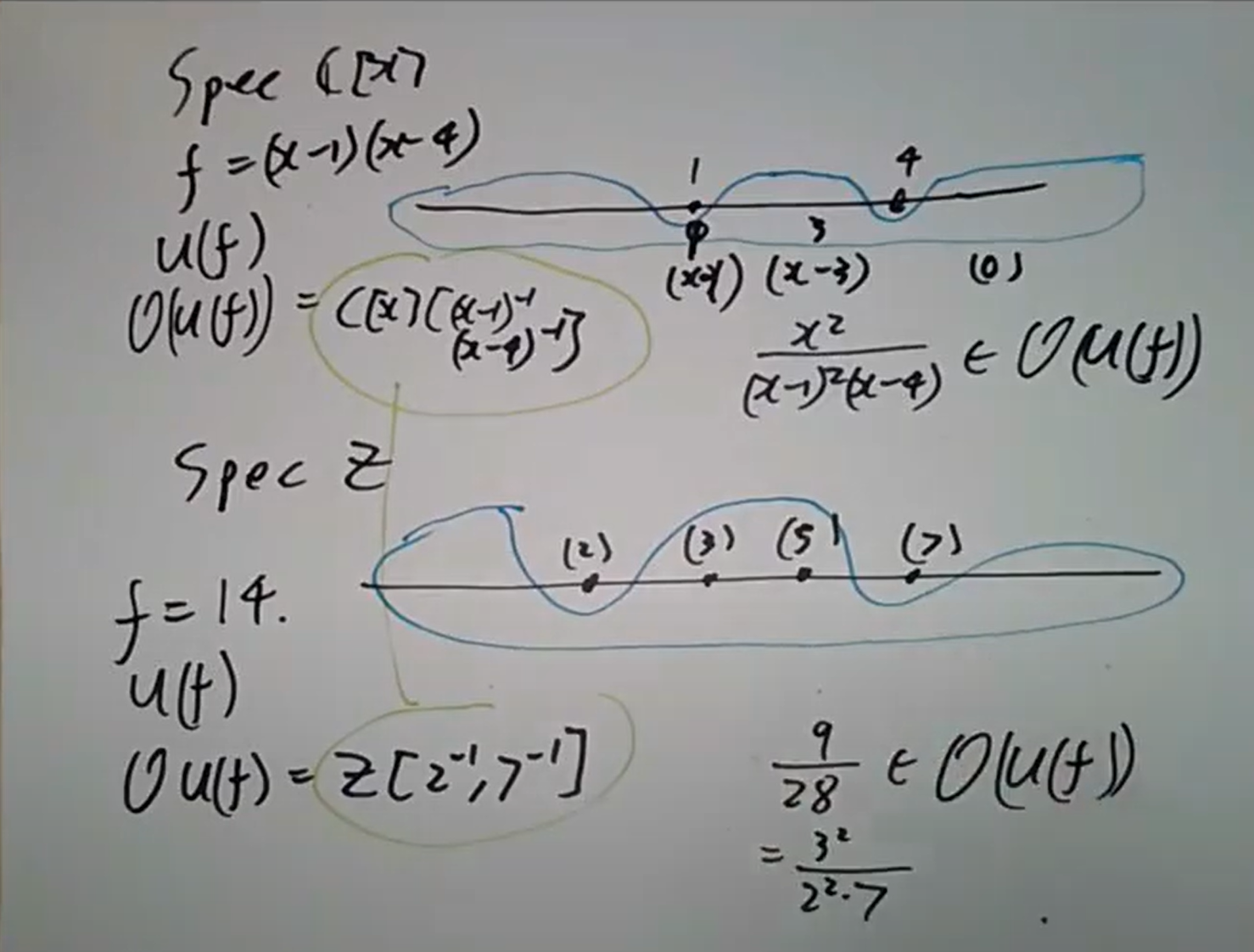
Exercise: 2.19, 2.26
Exercise for the ambitious: Check the sheaf property discussed in the lecture for rings with zero divisors. (This is tricky.)
关于Matplotlib
Matplotlib大量使用numpy,所以两者经常被一同import
1
2import numpy as np
import matplotlib.pyplot as plt
Pyplot 是 Matplotlib 的子库,提供了和 MATLAB 类似的绘图
API,能很方便让用户绘制 2D 图表。
IPython(从而Juypter
Notebook)有一组预先定义好的所谓的魔法函数(Magic
Functions),你可以通过命令行的语法形式来访问它们,例如%matplotlib inline可以省略掉matplotlib.pyplot.show()。
Matplotlib同时支持命令式编程(作用于最近的图表或轴)和面向对象编程,推荐使用后者。
Matplotlib中定义了Figure容器
1
class matplotlib.figure.Figure(figsize=None, dpi=None, *, facecolor=None, edgecolor=None, linewidth=0.0, frameon=None, subplotpars=None, tight_layout=None, constrained_layout=None, layout=None, **kwargs)
matplotlib.pyplot.figure(num=None, figsize=None, dpi=None, *, facecolor=None, edgecolor=None, frameon=True, FigureClass=<class 'matplotlib.figure.Figure'>, clear=False, **kwargs)返回一个Figure对象。
num为int或str,为图形的唯一标识符。figsize是(float,
float)形式的tuple,表示宽度和长度,单位英寸,默认[6.4, 4.8]。
Axes是一个矩形区域,这个矩形是基于figure坐标系统定义的。Axes也是matplotlib框架中一个重要的类对象,但首先要把它理解为figure中的一个子矩形区域。
Figure.add_axes(rect, projection=None, polar=False, **kwargs)返回向Figure中添加新的轴的Axes对象。rect为(left,
bottom, width, height)形式元组,(left,
bottom)表示添加的子区域左下角坐标,width和height为子区域宽度长度,它们都以在Figure宽度和高度中的占比表示。
Figure.subplots(nrows=1, ncols=1, *, sharex=False, sharey=False, squeeze=True, width_ratios=None, height_ratios=None, subplot_kw=None, gridspec_kw=None)向Figure添加一组子图,形如nrows×cols的矩形排布,返回一个figure和Axes。
Axes中有许多绘图的函数:
plot([x], y, [fmt], *, data=None, **kwargs)或plot([x], y, [fmt], [x2], y2, [fmt2], ..., **kwargs)
用于用于绘制线图和散点图。向 plot 提供单个列表或数组,matplotlib
会假设它是一系列 y 值,并自动生成 x
值。接受两个数组时则会将前者作为x后者作为y绘图。fmt为string类型可选项,可以有color,
marker, linestyle, linewidth, markersize。具体的功用如下:
Color为颜色
| Character | Color |
|-----------|----------|
| 'b' | Blue |
| 'g' | Green |
| 'r' | Red |
| 'c' | Cyan |
| 'm' | Magenta |
| 'y' | Yellow |
| 'k' | Black |
| 'w' | White |
marker为图中点的标记
| Character | Description |
|-----------|-----------------|
| '.' | Point marker |
| 'O' | Circle marker |
| 'x' | X marker |
| 'D' | Diamond marker |
| 'H' | Hexagon marker |
| 's' | Square marker |
| '+' | Plus marker |
linestyle为直线形式
| Character | Description |
|-----------|------------------|
| '-' | Solid line |
| '--' | Dashed line |
| '.' | Dash-dot line |
| ':' | Dotted line |
在函数调用里写ax.plot(drug_conc, response, color='r', marker='o', linestyle='-.')和写ax.plot(drug_conc, response, 'ro-.')有相同效果。
类似地还有:
scatter():用于绘制散点图
bar()/Barh():用于绘制垂直/水平条形图和水平条形图
hist():用于绘制直方图
pie():用于绘制饼图
imshow():用于绘制图像
例如
1
2
3
4
5
6
7
8
9
10
11names = ['group_a', 'group_b', 'group_c']
values = [1, 10, 100]
plt.figure(figsize=(9, 3))
plt.subplot(131)
plt.bar(names, values)
plt.subplot(132)
plt.scatter(names, values)
plt.subplot(133)
plt.plot(names, values)
plt.suptitle('Categorical Plotting')
plt.show()
会产生
ax.set_title (label, fontdict=None, loc=None, pad=None, y=None)可以给Axes对象设置标题。label是string,用于作为标题的文本。fontdict是一个dict,包括'fontsize’
'fontweight’,
'color’等控制标题性质的关键字。loc可以是{'center', 'left',
'right’}中一个。y和pad都是为浮点数。y表示标题的垂直轴位置(1.0为顶部)。如果None(默认值),则自动确定y以避免轴上的装饰符。pad是标题与坐标轴顶部的偏移量,以点为单位。
ax.set_xlabel(xlabel, fontdict=None, labelpad=None, loc=None)和ax.set_ylabel(ylabel, fontdict=None, labelpad=None, loc=None)分别用于设置x轴和y轴的标签。loc在
{'bottom', 'center', 'top’}/{'center', 'left', 'right’}中。
ax.set_xticks(ticks)或ax.set_yticks(ticks)可以设置x/y轴的刻度位置。ticks为float的list,包括诸刻度的位置。
ax.set_xticklabels(labels, fontdict=None)或ax.set_yticklabels(labels, fontdict=None)可以设置x/y轴的刻度标签,labels为string的list。
ax.set_xlim( left=None, right=None)或ax.set_ylim( left=None, right=None)可以设置x/y轴的视图限制。
ax.set_facecolor(color)设置图表空白的颜色。
ax.set_frame_on(b)按布尔值b确定是否设置图表矩形边框。
ax.grid(b=None, axis='both’)设置网格线,axis可以为{'both',
'x', 'y'}中一个,表示某轴是否设置网格线。
Spiness是Axes的四个边框线,可以用ax.spines['right']、ax.spines['left']、ax.spines['top']、ax.spines['bottom']访问。
spine.set_color()可以设置颜色(None则不显示)。spine.set_linewidth()设置宽度。
ax.legend(labels, loc, fontsize, title, frameon…)在Axes对象中放图例。labels是str的list,是每条线的命名。而loc则是
ax.twinx()或ax.twiny()可以创建一个新的Axes,其中有一个不可见的x
/ y轴和一个独立的y / x轴,位于与原始轴相对的位置。