Borcherds交换代数网课的笔记
关于环与模
burnside多项式
对一般的不含幺环,我们某种意义上有办法把它变成一个含幺环,也就是“硬塞”一个新的单位元
unitization ,记为
注:unitization具有函子性,并且是
取
模
代数不变量
¢ ¢ ¢ ¢ f g g g f
也即
中的态射。
个
令
复形 指一系列 自由解消 ,合冲 。如果 长度 为
作为模或者理想有限生成
作为
作为域有限生成
诺特环
Reading Section (Eisenbud'c Commutative Algebra): 1.4
诺特环
诺特环
注意到
多元多项式环中理想的生成元数量并不能被未定元数控制。例如
Hilbert基定理
Reading: Section 1,4
(Hilbert)诺特环
对
诺特环
对
(Gordon,虽然称为Dickson引理)
证明
注:5.3的证明对任何有限生成的自由Abel群均适用。
事实上上面证明了
不变量的有限生成性
Reading: Section 1.5
利用基定理可以证明一些不变量的有限生成性,至少是对有限群
定义
注1:
注2:对满足 summand ,此时可以照搬上文证明
现在回到6.1的证明:取
注1:此处的论证适用于一大类分次环。对分次环
注2:一般分次环中
应当注意到Reynolds算子对任意群和任意域并非总是存在,例如
此外对非紧群
诺特模
Noether对定理6.2中
Reading: Section 1.7 (似乎实则应当1.11(?
诺特模
与诺特环的情形一致,我们有:
任何
任何子模的包含升链稳定
对模的正合列
只需证
诺特环上的有限生成模是诺特模。
诺特环上
令
事实上这还能进一步推广:
证明则是完全相同的。
这里的自由解消并不保证有限,也不保证唯一,但Hilbert证明了对一些特定环和其上的模,自由解消总是有限而且某种意义上几乎唯一,可以从分次自由解消中取出某种“最小”解消,然后其它自由解消就相当于在其基础上加上如
分次模 是形如分次自由 定义为一系列
分次自由解消 ,如果
则Hilbert的定理可以被陈述为:
这种消解的“几乎唯一”性给出了许多
不变量的有限生成性(续)
诺特证明了任意特征域上的
令
注:诺特的证明相比Hilbert对特征零情形的证明,难以推广到无限群的情形。
对更一般的情形,我们有定理:
如果
注1:Nagata证明了3推1,1推2某种意义上也是因为Nagata找到了一个G不是约化群时候不变量并非有限生成的例子,Haboush证明了2推3。
注2:条件3某种意义上在说存在一个非线性的Reynolds算子。在特征零的情况下,
注3(Borcherds猜测):
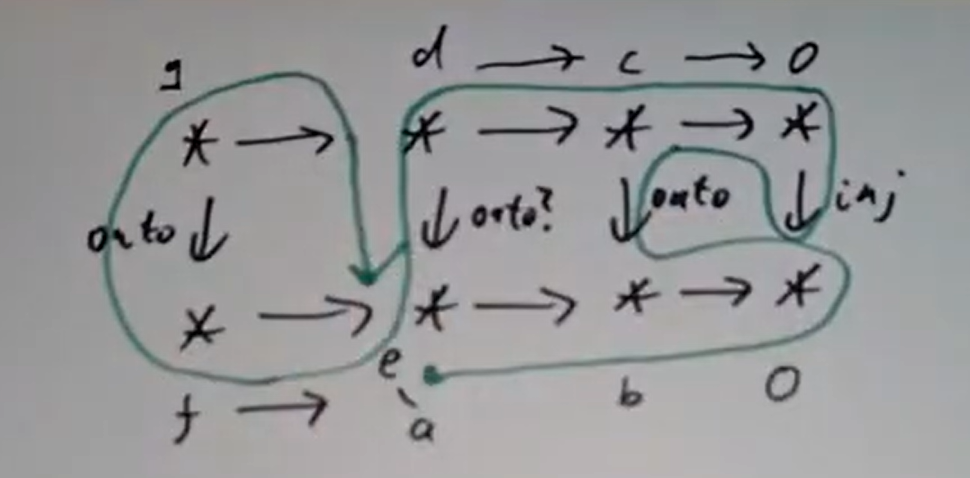 取
取 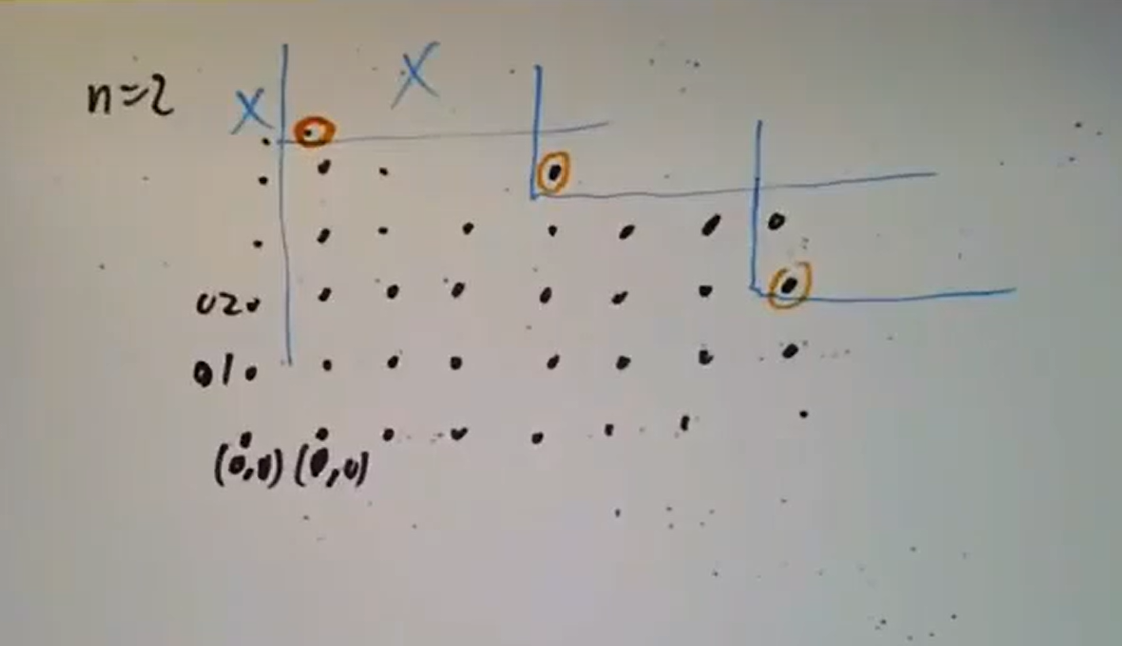 中一样将单项式列出,横轴为诸
中一样将单项式列出,横轴为诸 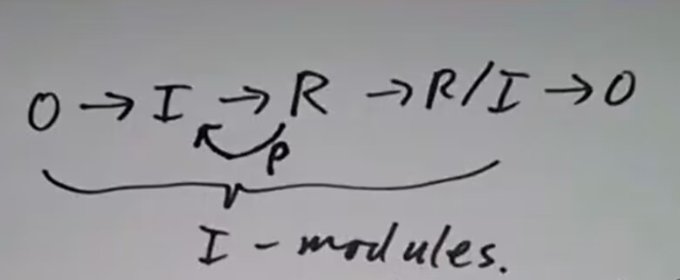 分裂,从而
分裂,从而

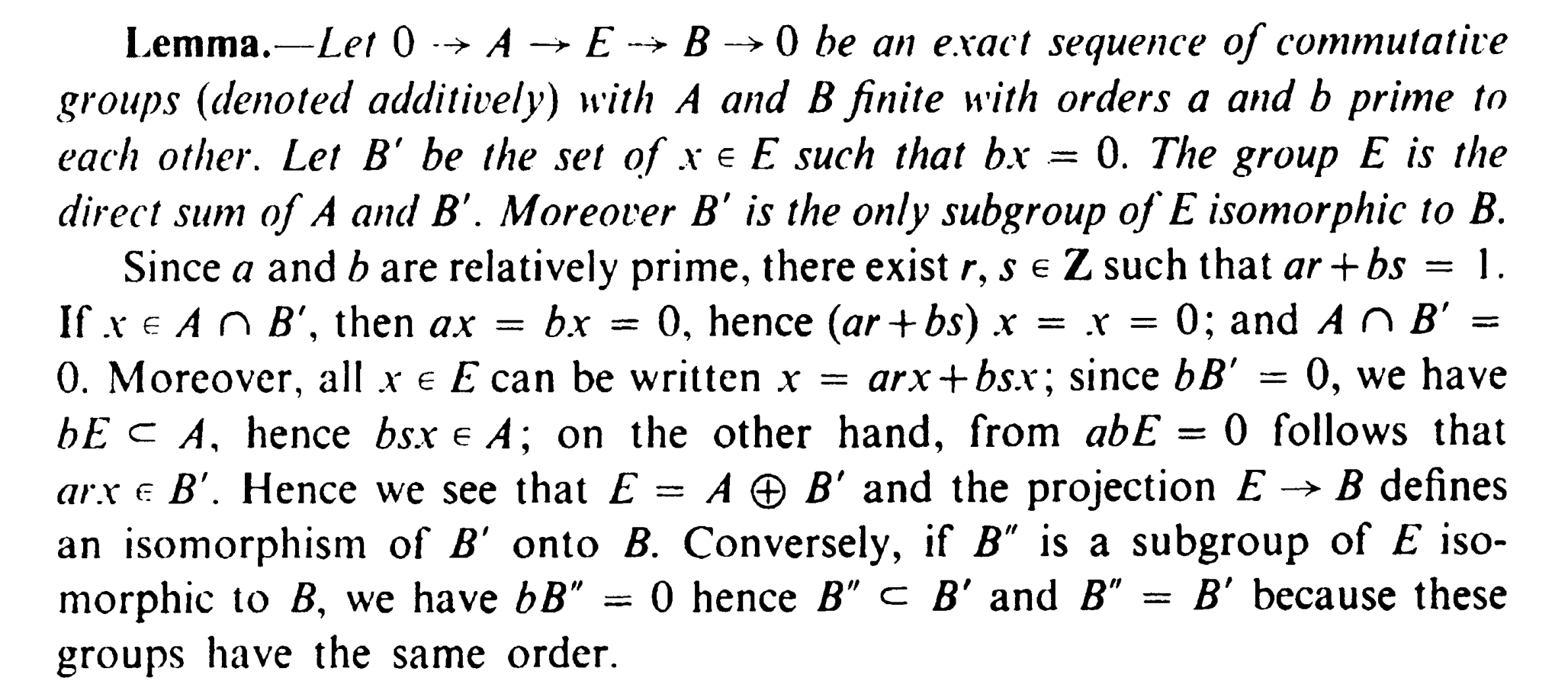 有
有