关于环的可视化,大体有三种比较直接的方法:画出环中每个元素、画出环的一组基和画出环的素理想。
环元素作为点的可视化
这种可视化适用于加群可嵌入线性空间的环,所以它对代数数域的代数整数环,从而对代数数论很有用。这种可视化最简单的例子如下
取
类似的方法可以毫无阻碍地推广到
不过这个问题可以一定程度上“修复”。例如考虑
某种意义上ED是稀有的,即使在UFD中也是如此。例如考虑
环一组基作为点的可视化
Exercises: 1.18, 1.19
如果我们的环像
只对
假设
域上多元形式幂级数环
考虑二元情况。假设
注1:我们不能希望像
注2:收敛幂级数环并非UFD。例如考虑一个有无穷多零点
环素谱的可视化
Exercises: 1.24
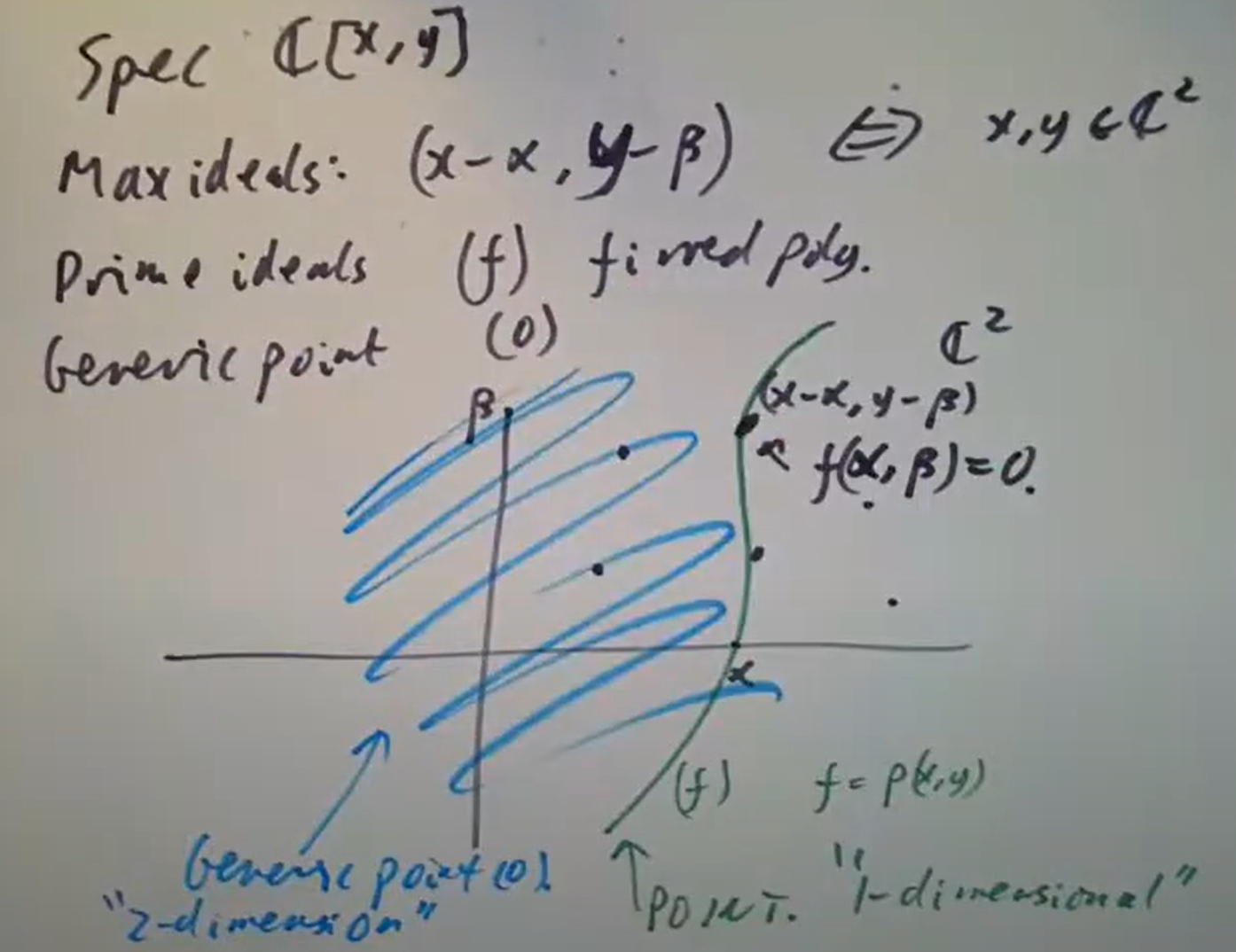
引入素谱的动机从一类特殊的环说起。对紧Hausdorff空间
具体来说,首先证明
这种漂亮的对应我们希望也能推广到任意环上,于是得到了所谓环的极大谱,但有一个问题是极大谱不具有函子性(极大理想的原像不一定是极大理想,如
素谱
Exercises: 1.13, 1.14
素谱的拓扑
环
注:拟紧和紧的定义完全一致,叫这个名字只是因为20世纪50年代拟紧被定义时,紧经常指紧Hausdorff。
Exercises: 1.10, 2.256 -1), the group ring of the cyclic
group of order 6.
不可约空间
不可约 ,如果
不可约是极强的性质,而且高度非Hausdorff,事实上Hausdorff且不可约等于说
假设
对全体包含
事实上假设
但非闭的素理想则会变得奇异。考虑如此构造:取某个非孤立点
Exercises: 1.9, 1.11, 1.25
诺特空间
诺特 ,如果下列等价条件成立:
诺特环
考虑到
Hausdorff和诺特是高度不相容的性质。
若Hausdorff空间
只需证
(Noetherian induction)假设
取所有不满足
诺特空间中的闭集皆为有限多不可约闭集的并
令
取
现在考虑
Exercises: 1.2
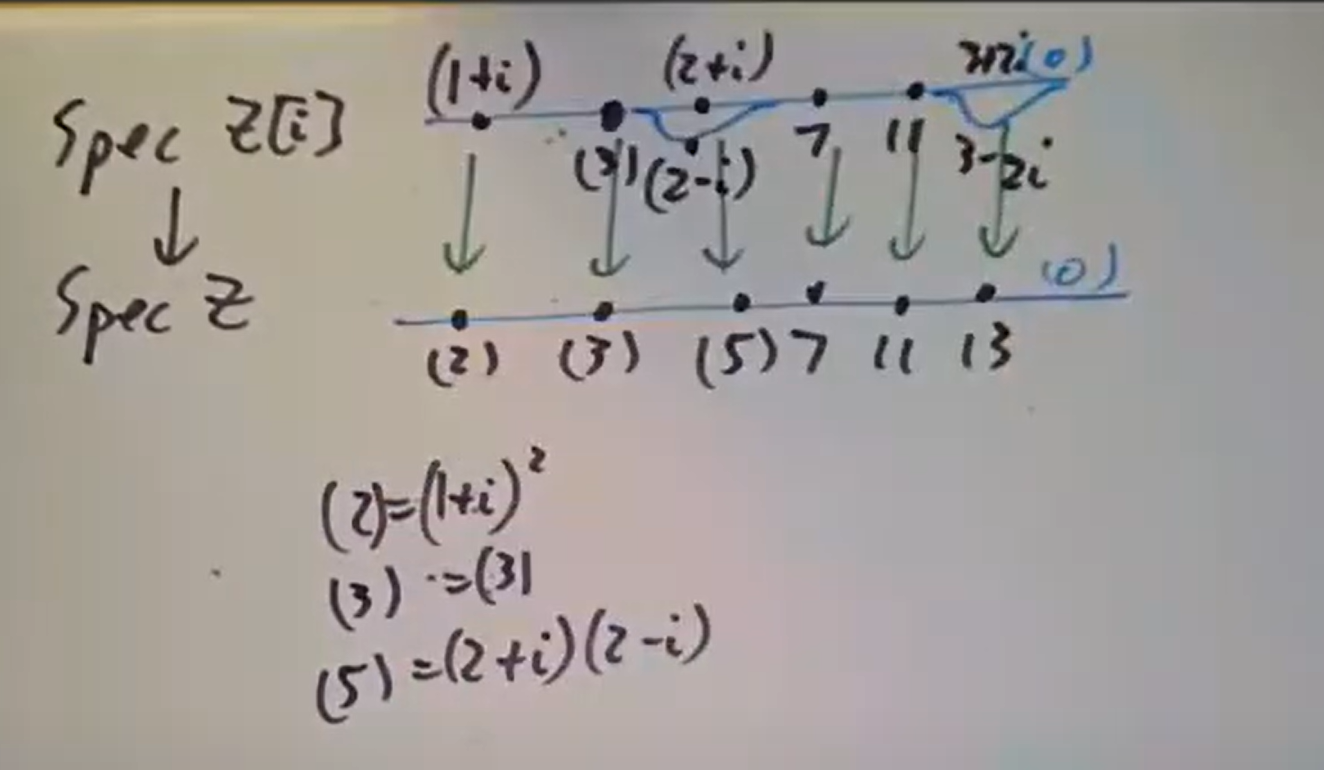
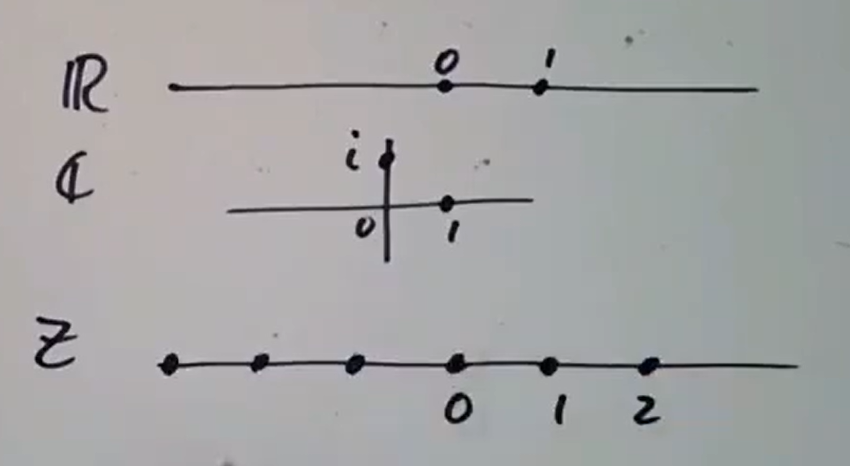 此外有高斯整数
此外有高斯整数  这种可视化手段的一个直接应用是:
这种可视化手段的一个直接应用是: 则立即可知上述
则立即可知上述 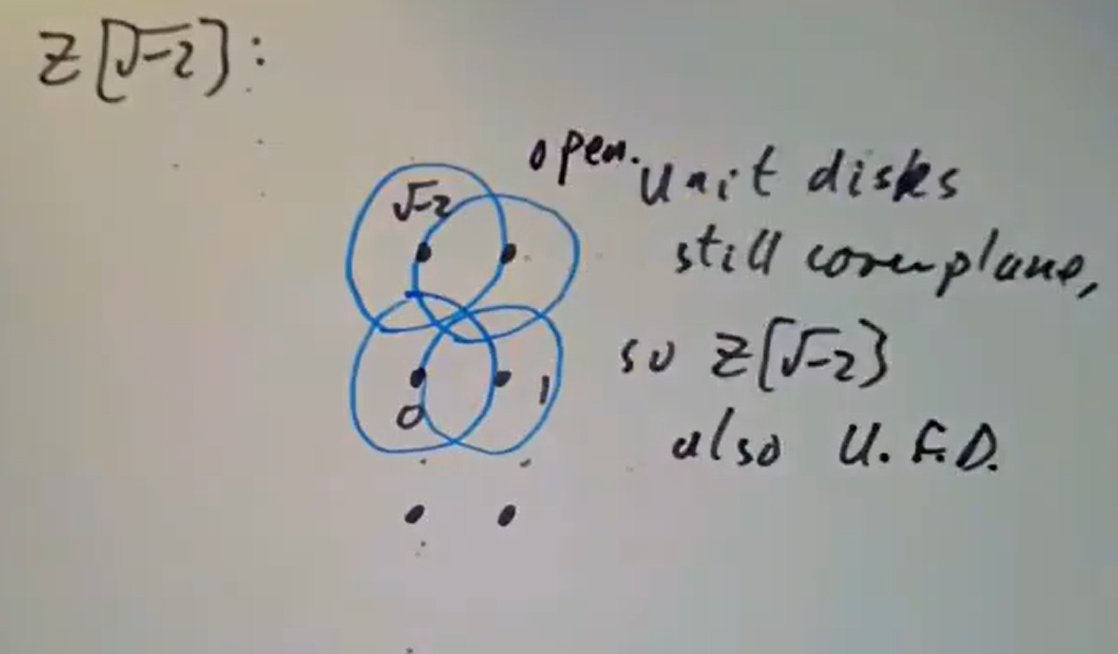 画图立即可知。
画图立即可知。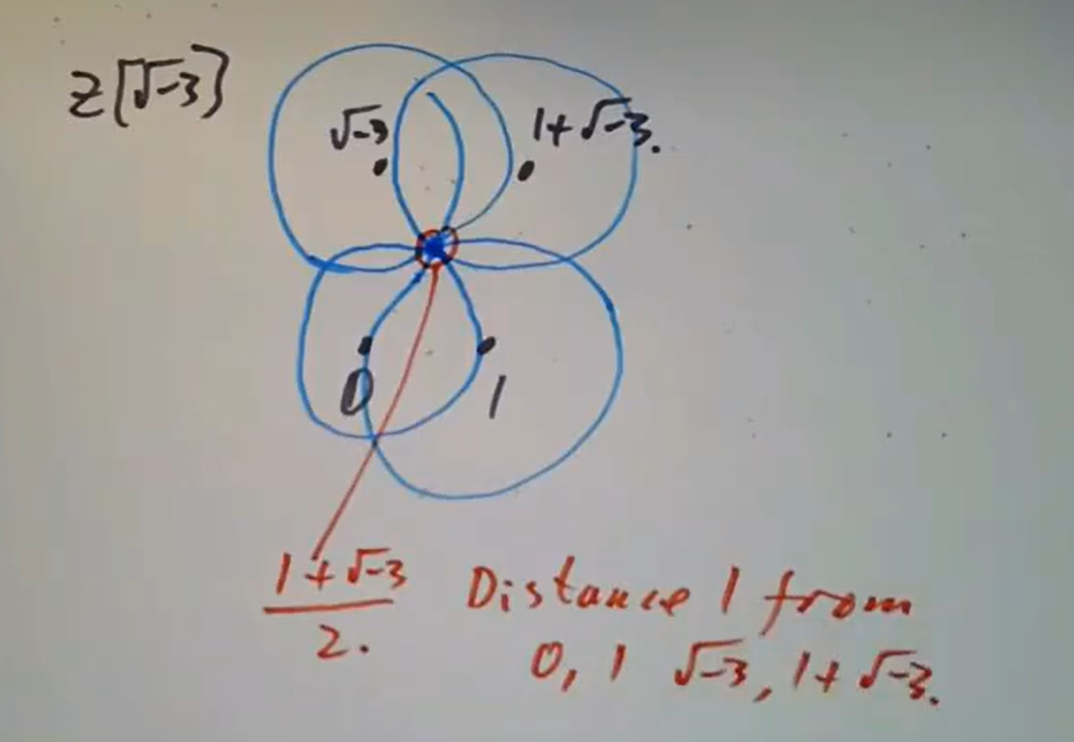 非但如此,
非但如此,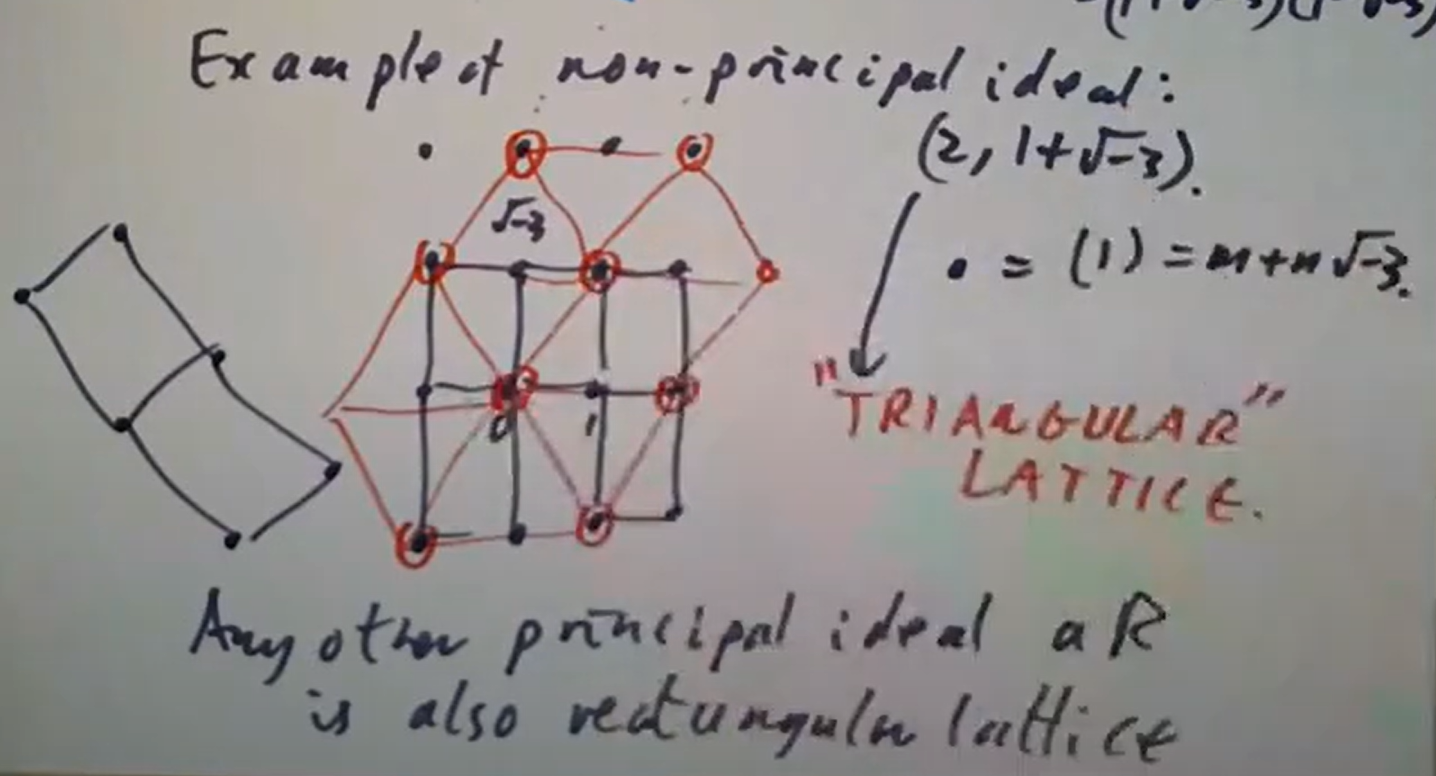 这里
这里 
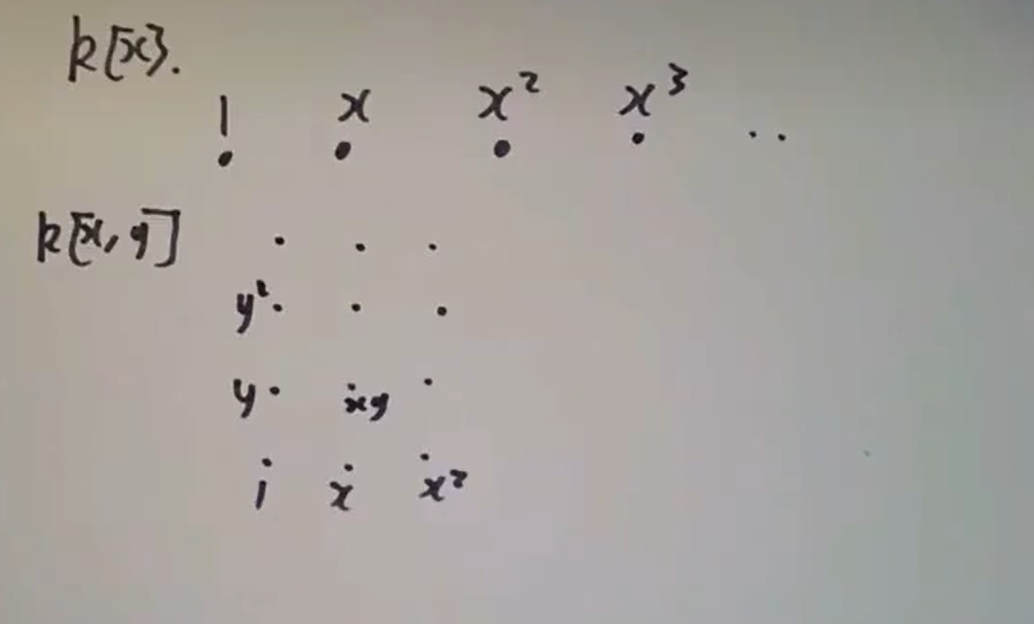
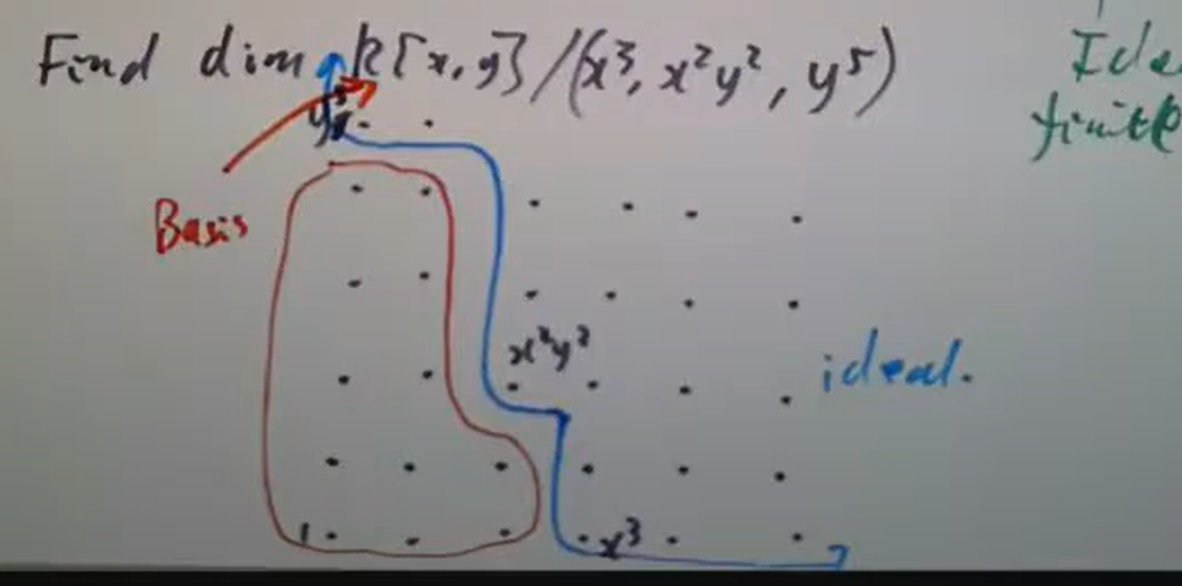 红圈中的元素便给出商环的一组基,于是立即可知
红圈中的元素便给出商环的一组基,于是立即可知  注意到不变量环同构于
注意到不变量环同构于 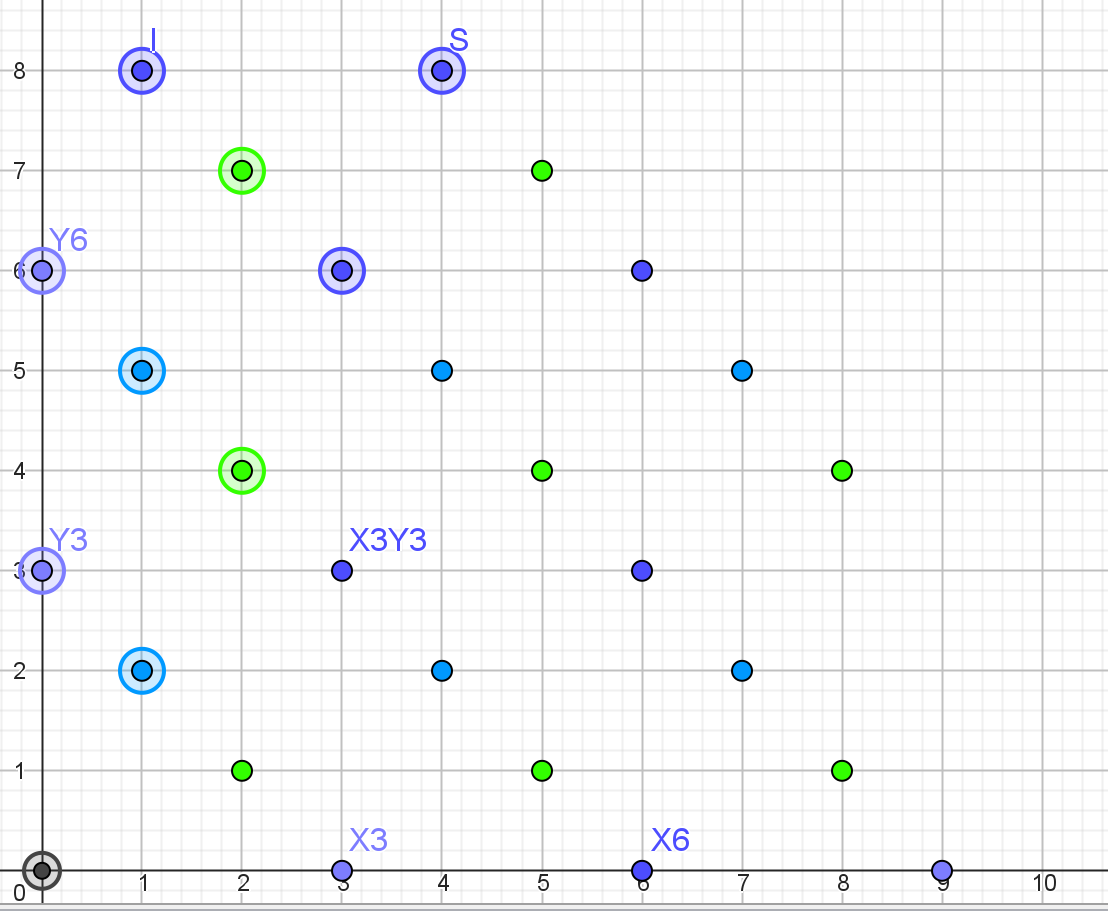
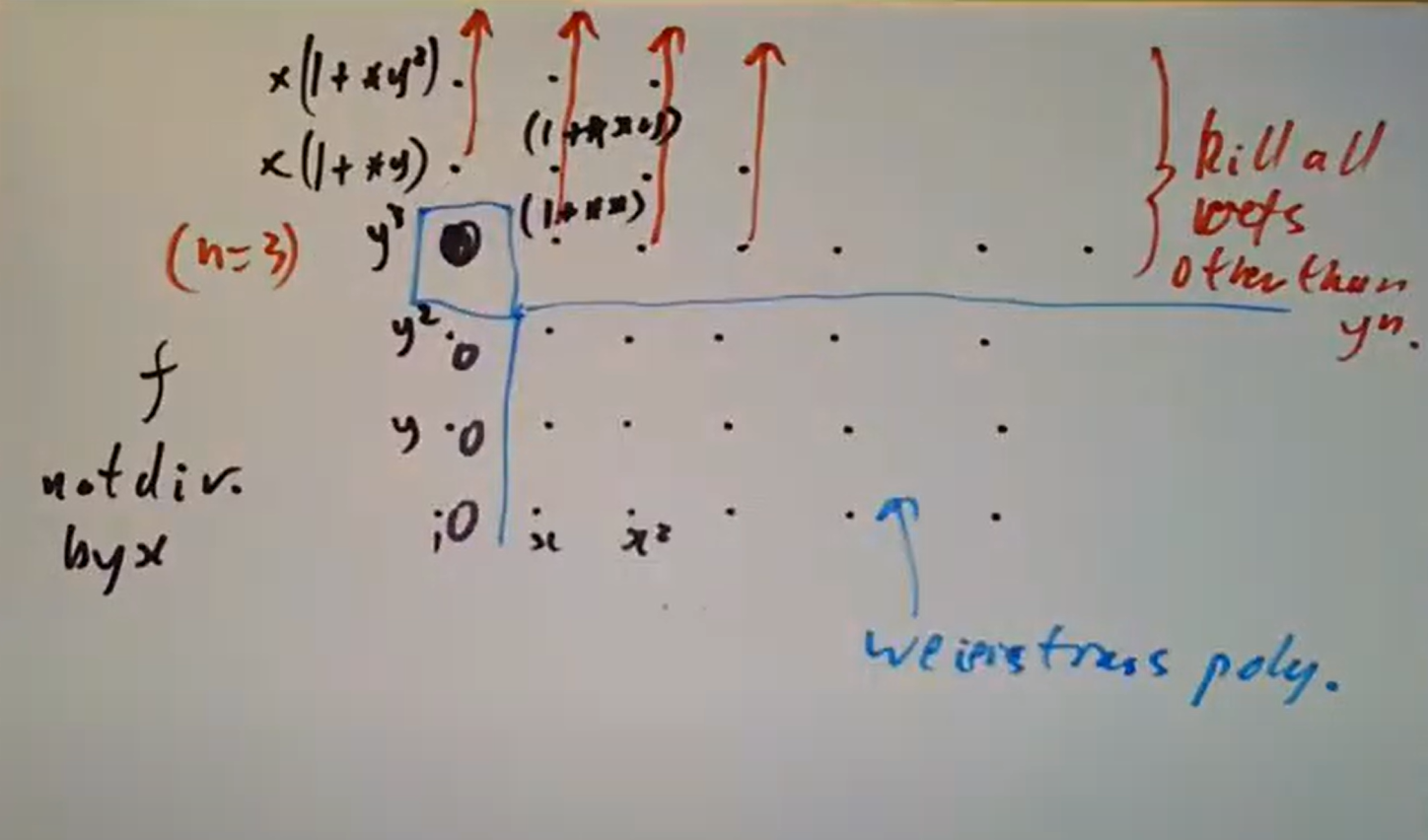 这样下来乘上这些元素的无穷乘积即可消去诸
这样下来乘上这些元素的无穷乘积即可消去诸 
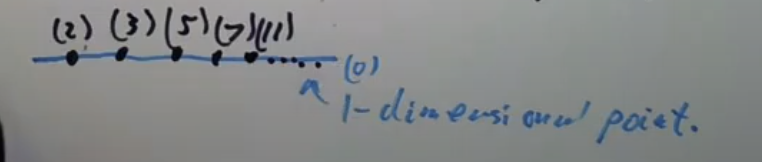



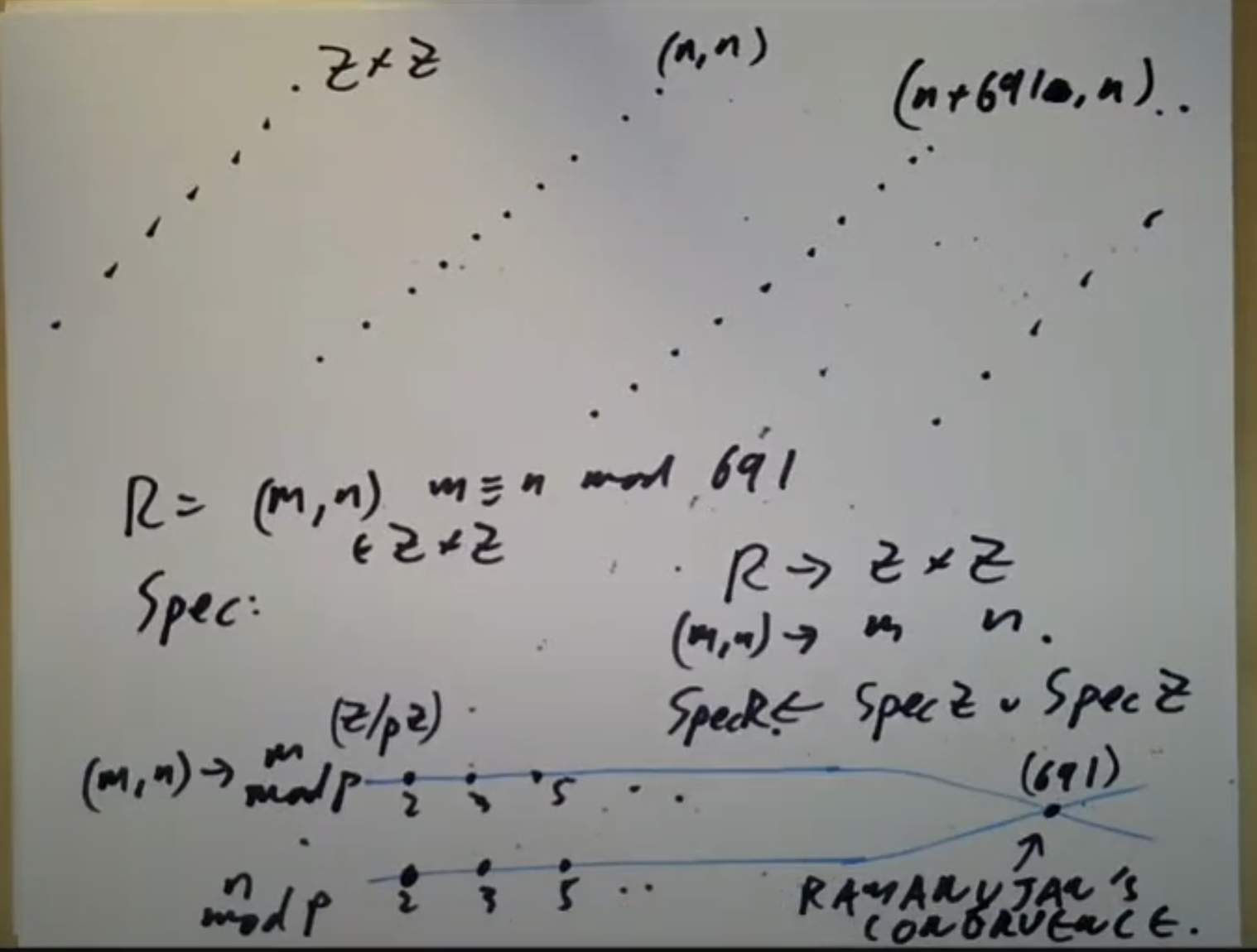 像691这样的素数被称为Eisenstein素数。
像691这样的素数被称为Eisenstein素数。

 总共这里有四个不可约分支,对应四个
总共这里有四个不可约分支,对应四个 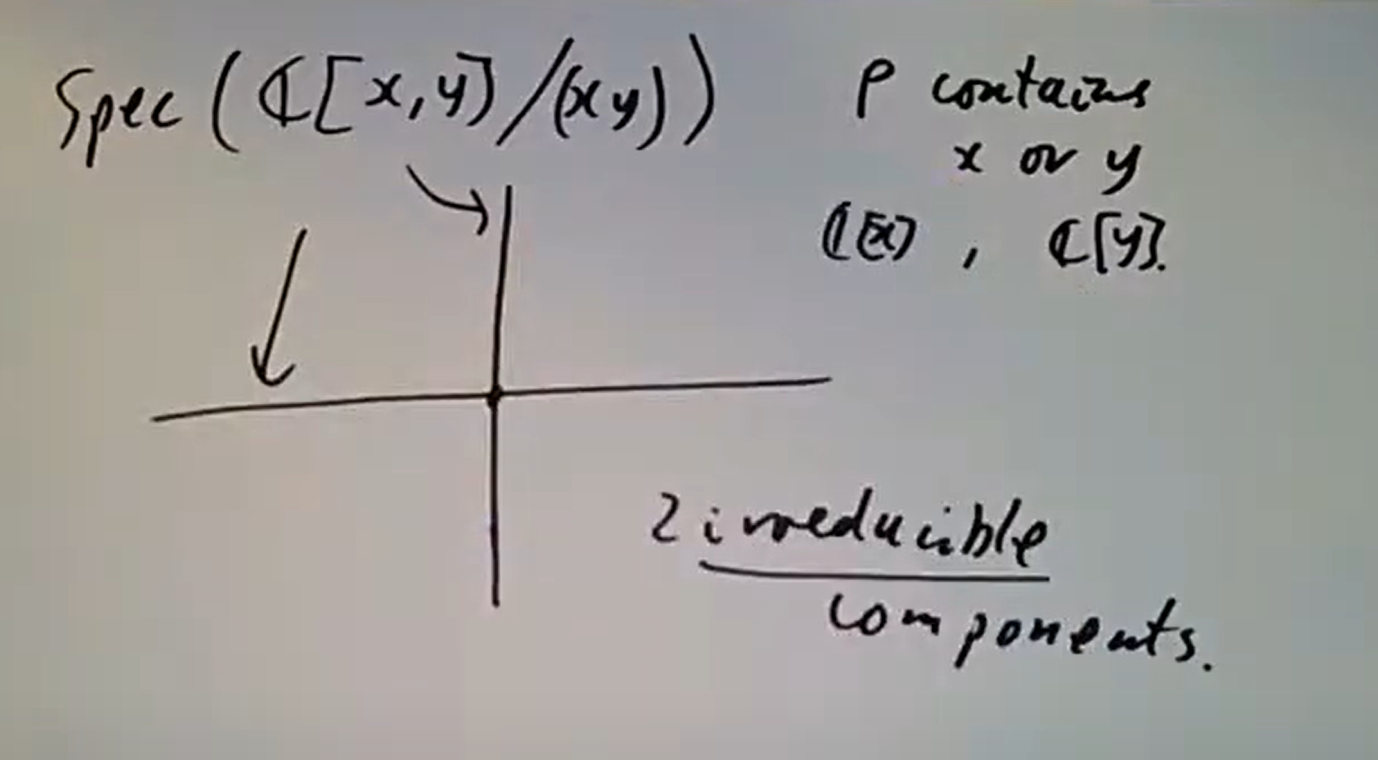
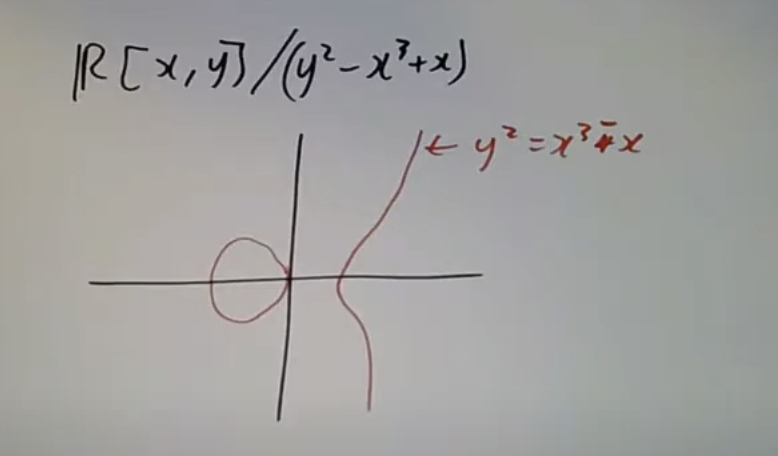
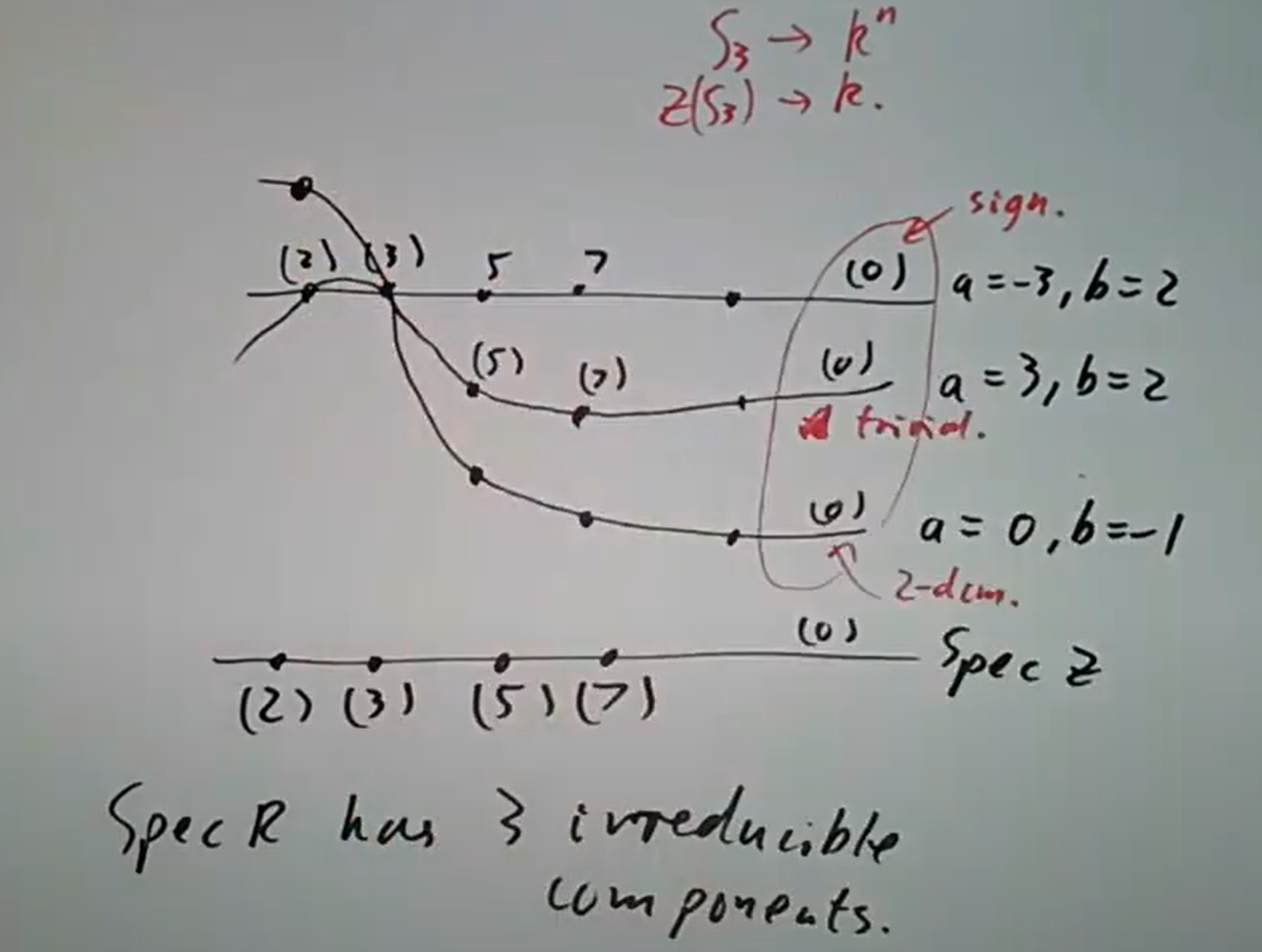 三个不可约分支对应三个
三个不可约分支对应三个